What is the tension force at the top of a spring?

[Cloruro de potasio]

Good afternoon,

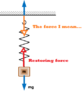
I have some doubts about the tension force suffered by a spring to which a mass is hung and which is making a simple vertical armoin movement. My doubt lies in the fact that at the bottom of the pier (where the mass hangs), the spring exerts the restoring force that is given by Hooke's Law. However, at the top of the dock (at the point where it is fixed), what is the tension force that appears? Is it the same as the restoring force but in the opposite direction?

Thanks in advance

 

[BvU]

Ask yourself what it is in equilibrium: the restoring force is zero (at least that is my perception of a restoring force ...) but the suspendion point has to exert an upward force !

And when the mass is oscillating up and down, you first ask if the spring is massless. If it is, a simple force balance tells you the answer to your question !

 

[Cloruro de potasio]

Thanks for your answer,

What I mean by restoring force is the force given by Hooke's Law, in the system we are studying, that force would be given in the opposite direction to elongation, what I don't understand very well is the force that has to It appears at the point of contact between the spring and the surface, I have measured it experimentally with a PASCO sensor, and I get that it is equal to the restoring force but in the opposite direction, why does this happen?

 

[Chestermiller]

This is very hard to decipher. Can you possibly show the equations?

 

[BvU]

why does this happen?

Apparently -- according to your observations -- the spring mass can be ignored. The whole thing stays in place (a=0), so there must be an equilibrium between the external forces.

Were your measurements done while the mass was going up and down, or in equilibrium situations ?

 

[Cloruro de potasio]

This is very hard to decipher. Can you possibly show the equations?

The question is that the only equation I can think of is Hooke's Law, but I don't understand why the force that reads the sensor is exactly the same as the restoring force but in the opposite direction (as the sensor is at the point of contact of the spring with the surface, this must be the force that feels the point of contact of the spring with the surface, something similar to the tension in a system in which a body hangs on a rope) there must be some consideration relative to the third Law of Newton, or something like that escapes me ...

 

[Cloruro de potasio]

Apparently -- according to your observations -- the spring mass can be ignored. The whole thing stays in place (a=0), so there must be an equilibrium between the external forces.

Were your measurements done while the mass was going up and down, or in equilibrium situations ?

In both ways, I studied both the static and the dynamic method, in both cases the same thing happened, the force determined by the sensor was in the same direction as the elongation ...

 

[BvU]

I get that it is equal to the restoring force but in the opposite direction

the force determined by the sensor was in the same direction as the elongation

What did the sensor measure ? The force exerted by the suspension, or thte force exerted by the spring on the suspension point ?

 

[Cloruro de potasio]

Thanks again, the sensor mediates the force exerted by the spring on the suspension. If we think about it slowly, it makes sense that this force goes in the opposite direction than the restoring force given by Hooke's Law, but I don't know very well how to explain it from a formal point of view ...I enclose the same diagram you show in your response with the force to which I refer to...

 

[BvU]

but I don't know very well how to explain it from a formal point of view

It's simple Newton: Your forces exerted by the spring are equal and opposite to the forces on the spring (Newton 3). And if they were not equal in magnitude, the spring would accelerate away (Newton 2) -- which it doesn't do. A case of $F = ma$ ($m$ the mass of the spring itself) with $a$ going very big if $m$ is very small.

Take a rubber band and hold the ends. You can't pull with different magnitude forces. Same with a rope or a rod ($k \approx \infty$).

 

[Cloruro de potasio]

Okay, thank you very much, I think I understand something better now, what I have not seen is the reason why the forces have to balance, after all the lower part of the pier if it is suffering an acceleration .. .

Is the diagram that I attached with the value of the different forces correct?

 

[A.T.]

Okay, thank you very much, I think I understand something better now, what I have not seen is the reason why the forces have to balance, after all the lower part of the pier if it is suffering an acceleration .. .

If the mass m is oscillating, then so is the center of mass of the spring. So if you don't assume a mass-less spring, the forces on the spring are not balanced.

Is the diagram that I attached with the value of the different forces correct?
View attachment 254595

It's not clear which force acts on which body.
It's not clear if the spring has any mass.
The red force is missing its Newtons 3rd Law partner.
The 2 forces at the upper attachment must satisfy Newtons 3rd Law (equal but opposite), but in a dynamic situation there is no reason to assume -mg acting at the ceiling.

 

[Cloruro de potasio]

Thanks again, the mass of the pier is not zero, but if it is very small compared to the masses that are placed on the pier, I still don't quite understand the reason why the force exerted by the spring on the surface is equal to the restoring force given by Hooke's Law, but in the opposite direction ...

I have tested it experimentally both in the static and dynamic case and in both cases the same happens (attached a graph obtained from force and position sensors)

This is the position:

This is the force:

 

[vanhees71]

Hm, that's not very surprising since from
$$\ddot{x}=-\omega^2 x$$
the general solution is
$$x(t)=x_0 \cos(\omega t) + \frac{v_0}{\omega} \sin(\omega t),$$
and the force is thus proportional to the elongation,
$$F=m \ddot{x}=-m \omega^2 x.$$
Since the force is in phase (not shifted by $\pi$, i.e., not with the sign) you obviously measure not the force acting on the body but the reaction force on the suspension.

 

[Cloruro de potasio]

Yes, thank you, I understand that measure the reaction force, it is something logical by the way in which the sensor was placed, what I cannot understand from a physical point of view is the reason why this force is the same but in the opposite direction to Hooke's Law

 

[A.T.]

what I cannot understand from a physical point of view is the reason why this force is the same but in the opposite direction to Hooke's Law

Newton's 3rd Law.

 

[Cloruro de potasio]

But... how do you apply Newton's Third Law to this system??

 

[vanhees71]

Yes, thank you, I understand that measure the reaction force, it is something logical by the way in which the sensor was placed, what I cannot understand from a physical point of view is the reason why this force is the same but in the opposite direction to Hooke's Law

That's Newton's 3rd postulate.

 

[A.T.]

But... how do you apply Newton's Third Law to this system??

force_by_spring_on_ceiling = - force_by_ceiling_on_spring
force_by_spring_on_mass = - force_by_mass_on_spring

 

[Mister T]

I still don't quite understand the reason why the force exerted by the spring on the surface is equal to the restoring force given by Hooke's Law

It's a tautology. When you make the assumption that Hooke's Law is valid for the spring you assume Hooke's Law gives you the force exerted by the spring.