birdgirl
- 5
- 0
[SOLVED] Wien Bridge Frequency Proof
The ac bridge circuit shown is called a Wien bridge (also Wein bridge).
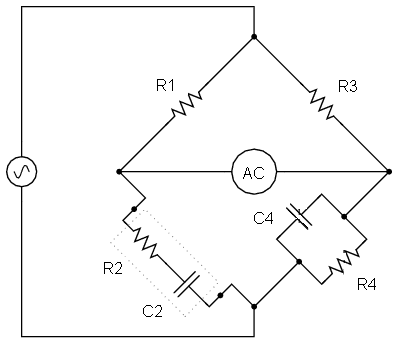
Show that when the bridge is balanced, frequency is found by the Eqn attached.
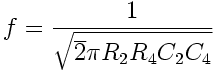
w=2*pi*f
Using the number from each branch as a guide, the general solution to AC bridges is Z4 = (Z3/Z1)*Z2
I keep trying to solve for impedences to plug into the second equation provided, but my j values do not cancel and the equation left is rather messy (R2R4C2C4*w^2 +jw(RzR4C2 -R2C2 -R4C4) +1 = 0.
For my impedence values I have been using
Z1 = R1
Z2 = R2 -j/wC2
Z3 = R3
Z4 = (R4/jwC4)/(R4 +jwC4)
Any help with this would be greatly appreciated.
Homework Statement
The ac bridge circuit shown is called a Wien bridge (also Wein bridge).
Show that when the bridge is balanced, frequency is found by the Eqn attached.
Homework Equations
w=2*pi*f
Using the number from each branch as a guide, the general solution to AC bridges is Z4 = (Z3/Z1)*Z2
The Attempt at a Solution
I keep trying to solve for impedences to plug into the second equation provided, but my j values do not cancel and the equation left is rather messy (R2R4C2C4*w^2 +jw(RzR4C2 -R2C2 -R4C4) +1 = 0.
For my impedence values I have been using
Z1 = R1
Z2 = R2 -j/wC2
Z3 = R3
Z4 = (R4/jwC4)/(R4 +jwC4)
Any help with this would be greatly appreciated.