What mass must be placed on the cord to keep the pulley from rotating?

[I_Try_Math]

Homework Statement

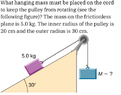
What hanging mass must be placed on the cord to keep the pulley from rotating (see the following figure)? The mass on the frictionless plane is 5.0 kg. The inner radius of the pulley is 20 cm and the outer radius is 30 cm.

Relevant Equations

$\tau = rFsin\theta$

I suppose to keep the pulley from rotating the net torque has to be zero?
Let $F_{r}$ be the force that the 5 kg mass on the ramp exerts on the pulley and $F_{d}$ be the force exerted straight down by the other mass on the pulley.
Let $r = 0.3$ m be the outer radius of the pulley.
$\sum \tau_{i} = F_{r}rsin90 - F_{d}rsin90 = 0$
$F_{r}r - Mgr = 0$
$r5gsin30 - rMg = 0$
$\Rightarrow M = 2.5 kg$

I'm wondering if I solved for $F_{r}$ incorrectly? Or there's some other mistake? Any hints are appreciated.

 

[haruspex]

It is very unclear, but it looks to me that the two cables are at different distances from the centre of the pulley. This suggests that the two radii given refer to two different wheels side by side on the same pulley. The drawing shows a dark inner annulus and lighter grey outer annulus.