What mistake did I make in finding the reaction at hinge A?

[gnits]

Homework Statement

To find forces in a framework

Relevant Equations

Equating of forces
Moments

A very simple (I thought!) question:

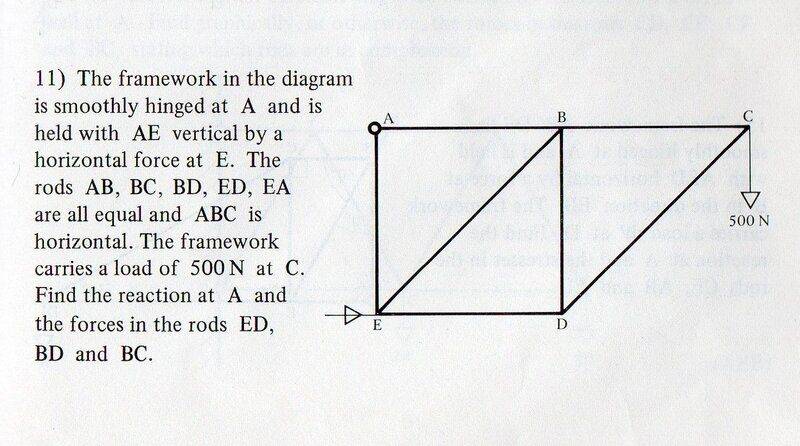
I'm just looking at the first part, finding the reaction at the hinge A.

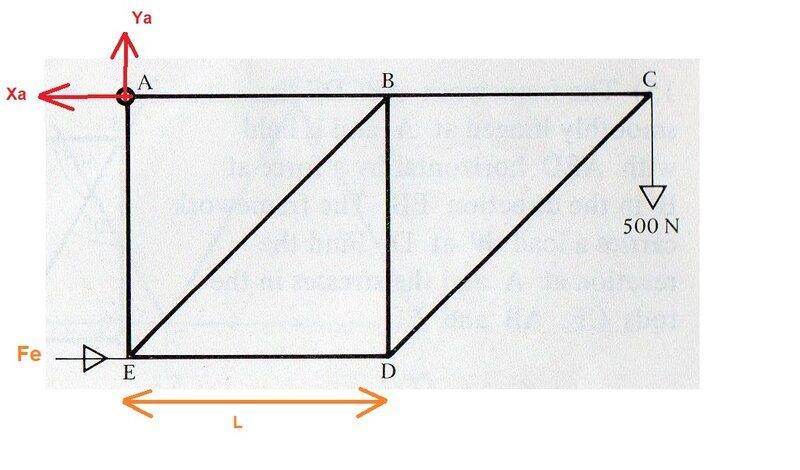
Here is my annotated diagram, with the reaction and A resolved into it's X and Y components, the force at E labelled as Fe and the length of ED labelled as L.

Considering the body as a whole:

Resolving vertically:

Ya = 500

Taking moments about E:

Xa * L = 2 * L * 500

which gives Xa = 1000

So the resultant at A will have size sqrt(1000^2 + 500^2) = 1118 (approx.)

Answer given in book is 112 N at 26.6⁰ below the horizontal.

My answer is very different and also above the horizontal.

What simple mistake have I made in my reasoning?

Thanks.

 

[Lnewqban]

The answer given in the book is not correct, yours is.

 

[gnits]

Thanks, that's a relief. The book has rarely been wrong and so I was all too ready to doubt myself. Much appreciated.

 

[haruspex]

Thanks, that's a relief. The book has rarely been wrong and so I was all too ready to doubt myself. Much appreciated.

The book's error in the magnitude is clearly just a decimal place blunder.
Above or below horizontal is inadequate to define the direction. Given the angle it makes to the horizontal, there are four possible directions. Up and to the left can be thought of as above horizontal, viewing it as a motion in that direction from A. But it can be viewed as below horizontal when considering the diagonal line through A that it lies on: first and third quarters = above horizontal, second and fourth quarters = below horizontal.