shinwolf14
- 14
- 0
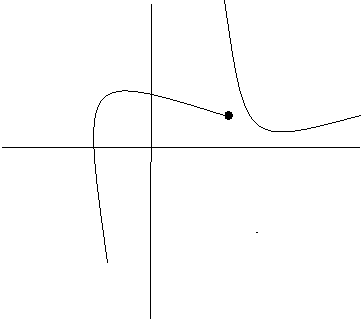
Hello everyone. I am currently having trouble actually defining what qualifies as an infinite discontinuity. I have read several sources that state that both of the one sided limits must approach infinity (positive, negative or both). My problem is what happens when only one of the one sided limits approach infinity and the other is finite. This is not a jump discontinuity because both of the one sided limits are not finite. According to the definition that I have read, it doesn't qualify as an infinite discontinuity either. I have crudely drawn what I am trying to describe. I am pretty sure this still is classified as an infinite discontinuity but I just wanted to be sure.