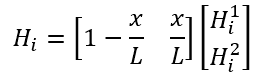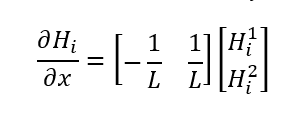The discussion centers on understanding the differential of a specific expression involving the partial derivative \(\frac{\partial H_i^j}{\partial x}=0\). Participants seek clarification on the physical meaning of this equation and its implications in a broader context. The inquiry emphasizes the need for a deeper investigation into the first 4x4 quantity related to this differential, indicating its significance in the relevant field of study.
PREREQUISITESStudents and professionals in physics, mathematicians specializing in differential equations, and researchers exploring tensor analysis and its applications in theoretical frameworks.
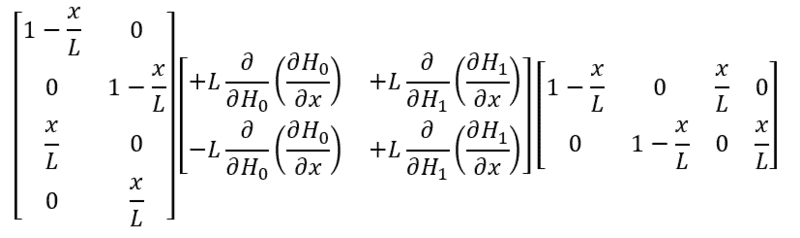From these equations it seems \frac{\partial H_i^j}{\partial x}=0 holds. Could you tell me physical meaning or background of the first 4x4 quantity for further investigation ?ssafdarpk said:where
Now what I can understand the differential of
