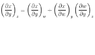Where did this equation come from?
- Thread starter pivoxa15
- Start date
Click For Summary
SUMMARY
The discussion centers on the derivation of a mathematical identity in thermal physics involving the equation x(y,z) = x(y,w(y,z)). Participants clarify that the variables x, y, z, and w are dependent variables, with w potentially being a function of both y and z. The conversation emphasizes the use of the chain rule for partial derivatives and the necessity of understanding the Jacobian when transitioning between variable representations. The notation used in physics is noted as being less clear than in mathematics, which adds complexity to the derivation process.
PREREQUISITES- Understanding of partial derivatives and the chain rule
- Familiarity with the concept of dependent and independent variables
- Knowledge of the Jacobian in multivariable calculus
- Basic principles of thermal physics and mathematical identities
- Study the application of the chain rule in multivariable calculus
- Learn about the Jacobian and its role in variable transformations
- Explore mathematical identities used in thermal physics
- Review examples of partial derivatives in physics contexts
Students and professionals in physics, mathematicians, and anyone interested in the application of calculus in thermal physics and mathematical derivations.
Similar threads
- · Replies 7 ·
- · Replies 7 ·
- · Replies 4 ·
- · Replies 13 ·
- · Replies 6 ·
- · Replies 4 ·