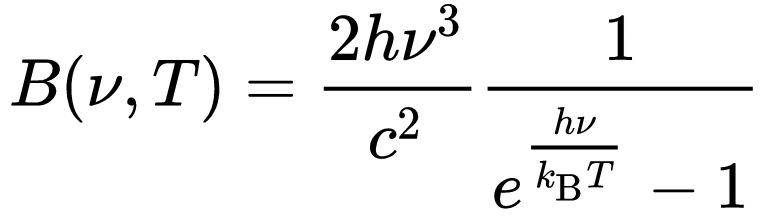SUMMARY
The discussion centers on the quantization term in Planck's Law, specifically addressing the misconception surrounding its existence. Participants clarify that the quantization aspect is not explicitly present in Planck's Law but is derived from the partition sum of the quantized electromagnetic field. The term "n" associated with quantization, akin to Bohr's model, does not apply here. For a deeper understanding, "The Conceptual Framework of Quantum Field Theory" by Duncan is recommended as a resource for the derivation of Planck's radiation law.
PREREQUISITES
- Understanding of Planck's Law and its application to Blackbody radiation.
- Familiarity with quantum field theory concepts.
- Knowledge of partition sums in statistical mechanics.
- Basic grasp of energy quantization principles (E=hf).
NEXT STEPS
- Study the derivation of Planck's radiation law in quantum field theory.
- Read "The Conceptual Framework of Quantum Field Theory" by Duncan for historical context.
- Explore the relationship between quantization and partition functions in statistical mechanics.
- Investigate the implications of energy discreteness in quantum mechanics.
USEFUL FOR
Students of physics, particularly those studying quantum mechanics and thermodynamics, as well as educators seeking to clarify concepts related to Planck's Law and quantization.
 Where do I find the quantization term (the "n") in Planck's Law?
Where do I find the quantization term (the "n") in Planck's Law?