Where to find this uniqueness theorem of electrostatics?

[coquelicot]

TL;DR Summary

Stating a nice uniqueness theorem of electrostatics, and asking for sources.

There is a nice uniqueness theorem of electrostatics, which I have found only after googling hours, and deep inside some academic site, in the lecture notes of Dr Vadim Kaplunovsky:

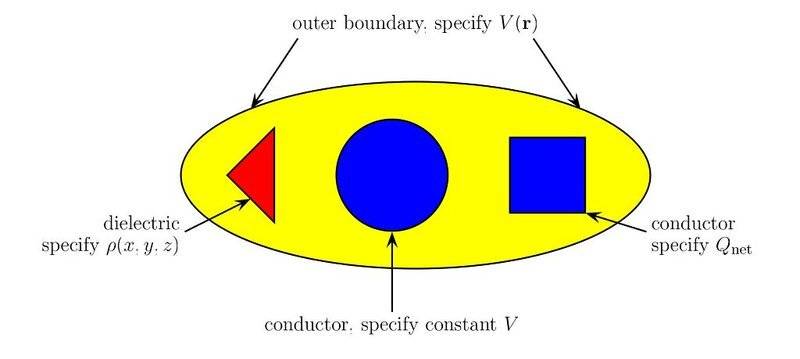
Suppose some volume $\Omega$ is not empty but contains several charged bodies, dielectrics or
conductors. For each conducting body, we specify either the net electric charge or the potential
(which is constant over a conductor). For each dielectric body, we specify the entire charge
distribution, i.e. $\rho (x, y, z)$ as a function of position within the body. Finally, we specify the
potential V (r) along the outer boundary S of the volume $\Omega$. Under these conditions, there
is a unique solution for the potential $V (x, y, z)$ inside $\Omega$ — including the dielectric and the conducting bodies themselves.

Notice that the important thing here is that only the NET charges on the conductors are specified, not their charge distributions (otherwise this would be nothing more than the uniqueness of the solution to the Poisson equation with mixed Dirichlet and Neumann boundary conditions).

This theorem is by no mean trivial, as seem to believe many authors that content themselves to invoke the "linearity and homogeneity of the equations of electrostatics" in many situations.
I have no idea if Dr Kaplunovsky demonstrated this theorem by himself, or if, more likely, he found it somewhere.
Are you aware of any book or reliable source where it can be found?

 

[pasmith]

You are solving multiple Poisson problems which are related to each other by the conditions on their common boundaries. The proof of uniqueness is therefore essentially the proof of uniquness for Poisson's equation, but with some further steps required by the internal boundary conditions. The possible boundary conditions are constrained to be of threee types, which makes the proof much simpler than it might otherwise be.

Assume $\phi_1$ and $\phi_2$ are two solutions satisfying the given boundary conditions. Then their difference $\phi = \phi_1 - \phi_2$ must satisfy $\nabla^2\phi = 0$ throughout $\Omega$ (because $\nabla^2 V_\phi = \nabla^2 V_\phi$ in every subregion of $\Omega$).

In each subregion $\Omega_i$ of $\Omega$ we have $$\begin{split} \int_{\Omega_i} \|\nabla \phi\|^2\,dV &= \int_{\Omega_i} \nabla \cdot (\phi\nabla \phi) - \phi\nabla^2 \phi\,dV \\ &= \int_{\partial \Omega_i} \phi \frac{\partial \phi}{\partial n}\,dS. \end{split}$$ Now if the final expression vanishes then $\|\nabla \phi\| = 0$ throughout $\Omega_i$ and hence $\phi$ is constant in $\Omega_)i$. We will show that the permissible internal boundary conditions together with outer boundary condition require that $\displaystyle\int_{\partial \Omega_i} \phi \frac{\partial \phi}{\partial n}\,dS = 0$ in each subregion and, morerover, that $\phi = 0$ in each subregion.

Let $\Omega_0$ be the part of $\Omega$ which is not on or in any dielectric or conductor. Then for $i \geq 1$:

• If $\Omega_i$ is a dielectric, then the boundary condition is that the potential is continuous, but the normal derivative jumps by a given value determined by the specified charge density $\rho$. It follows that $\dfrac{\partial \phi}{\partial n} = \dfrac{\partial \phi_1}{\partial n} - \dfrac{\partial \phi_2}{\partial n}$ jumps by zero, ie. it is continuous.
• If $\Omega_i$ is a conductor and the potential takes a specified constant value on the boundary then we must have $\phi = 0$ on this boundary since $\phi_1 = \phi_2$ here, so that $$\int_{\partial \Omega_i} \phi\frac{\partial \phi}{\partial n}\,dS = 0.$$ The same applies to the outer boundary where $\phi_1 = \phi_2 = V$ is specified.
• Otherwise, we have $$\int_{\partial \Omega_i} \frac{\partial \phi_1}{\partial n}\,dS = \int_{\partial \Omega_i} \frac{\partial \phi_2}{\partial n}\,dS = \frac{Q_{net}}{\epsilon}$$ and so $$\int_{\partial \Omega_i} \frac{\partial \phi}{\partial n}\,dS =0.$$ But since the potential is constant on the surface of a conductor we have on multiplying both sides by this value that $$\int_{\partial \Omega_i} \phi\frac{\partial \phi}{\partial n}\,dS = 0.$$

Let $\Omega'$ be the closure of $\Omega_0$ together with all dielectric subregions. Then on the boundary of $\Omega'$ we know that $\phi = 0$, and hence $\phi$ is constant in $\Omega'$. Continuity then requires that $\phi =0$. By continuity it now follows that $\phi = 0$ on and inside each conductor where only $Q_{net}$ is specified. For each conductor where a potential is specified, it is obvious that $\phi$ is constant inside the conductor and is equal to zero by continuity.

 

[Meir Achuz]

Isn't that theorem proved in many EM textbooks, with (of course) only the constant potential or total charge known on conductors?

 

[coquelicot]

Isn't that theorem proved in many EM textbooks, with (of course) only the constant potential or total charge known on conductors?

Not in my opinion. Or they think they have proved it but they are wrong: they usually invoke the linearity and homogeneity of the equations of electrostatics, but this proves only that the potentials are linear with respect to the charge distributions, not with respect to the net charges. This mistake seems to date as far as Maxwell.
Nevertheless if you can provide me a reference to this theorem, I'll be happy.

 

[coquelicot]

Assume $\phi_1$ and $\phi_2$ are two solutions satisfying the given boundary conditions. Then their difference $\phi = \phi_1 - \phi_2$ must satisfy $\nabla^2\phi = 0$ throughout $\Omega$ (because $\nabla^2 V_\phi = \nabla^2 V_\phi$ in every subregion of $\Omega$).

Not for the boundary conditions specified only by the NET charge, and that's the problem and the main source of error for many authors: When only the net charge is specified on a conductor, there might be two different charge distributions with the same net charge, whose difference would give rise a non zero $\nabla^2\phi$ on the boundary of these conductors. This destroys the rest of your proof if my understanding is correct (actually it may not be correct, because I don't understand your justification $\nabla^2 V_\phi = \nabla^2 V_\phi$. What is $V_\phi$ to begin with?)

There is a correct proof by Kaplunovsky here, not much more complicated than yours and a bit more explicit.
Do you have some reference for this theorem, with NET charge specified for conductors? (again, that's the main pitfall).

 

[pasmith]

Not for the boundary conditions specified only by the NET charge, and that's the problem and the main source of error for many authors: When only the net charge is specified on a conductor, there might be two different charge distributions with the same net charge, whose difference would give rise a non zero $\nabla^2\phi$ on the boundary of these conductors.

The charge in a conductor is always located on its surface and is evenly distributed there; otherwise there would be a current and the situation would not be static. Thus it is enough to specify the net charge, which results in a uniform surface charge density (the net charge divided by the surface area) and zero charge on the interior of the conductor.

 

[Meir Achuz]

results in a uniform surface charge density

This is not true. The surface charge adjusts to keep the conductor at constant potential.

 

[Meir Achuz]

the potentials are linear with respect to the charge distributions, not with respect to the net charges.

What does that mean?

 

[vanhees71]

The charge in a conductor is always located on its surface and is evenly distributed there; otherwise there would be a current and the situation would not be static. Thus it is enough to specify the net charge, which results in a uniform surface charge density (the net charge divided by the surface area) and zero charge on the interior of the conductor.

That's not entirely true. You can, e.g., analytically solve the problem of a conducting sphere and some point charge not located in the center of this sphere, using the mirror-charge ansatz. Then you'll find a non-uniform surface-charge distribution. You have to solve the Poisson equation for the given charge distribution and the boundary conditions for the conductor to get the electrostatic potential. The boundary conditions on the surface are that the potential and the tangential components of the electric fields are continuous across the surface, while the normal component jumps across the surface and the jump gives the surface-charge distribution along the surface. This is usually not uniform, as in the simple example with the sphere and the non-centrically located point charge (which may be inside or outside the spherical shell).

 

[coquelicot]

The charge in a conductor is always located on its surface

Indeed,

and is evenly distributed there;

Plain wrong. The charge will not be evenly distributed on the surface if the conductor is exposed to an exterior field.

otherwise there would be a current and the situation would not be static.

No, the field is normal to the surface of the conductor, and its tangential components are null, this is why the situation is static. This field is created by the exterior field, and the charges on the surface that distribute in such a way that it annihilate the tangential components of the exterior field.
That's why the following is not true:

Thus it is enough to specify the net charge, which results in a uniform surface charge density (the net charge divided by the surface area) and zero charge on the interior of the conductor.

NOTE: that's exactly the kind of pitfalls that many excellent authors are victim of.

 

[coquelicot]

What does that mean?

Let $\rho_i$ be the charge distributions on the surface of a given number of conductors, and let $V(x,y,z)$ be the potential they produced in the whole space. Now, assume that $\rho'_i$ are another charge distributions on the surface of these conductors, and that $V'_i$ is the potential they produce. Then it is trivial, from the linearity and homogeneity of the equations of the electrostatics, that the charge distributions $\rho_i + \lambda \rho'_i$ produce the potential $V + \lambda V'$, for every real number $\lambda$. In other words, the potential, and hence the potential of the various conductors, is linear with respect to the charge distributions. Unfortunately, we cannot induce from that that the potential is a linear function of the net charges of the conductors. For that, we need the aforementioned theorem that says that the net charge system is in 1-1 correspondence with the charge distributions.
This is where many authors are wrong. As a result, they assert incorrectly the existence of the capacitance matrix.

 

[Meir Achuz]

we cannot induce from that that the potential is a linear function of the net charges of the conductors.

Can you give an example of a nonlinear case?

 

[coquelicot]

Can you give an example of a nonlinear case?

No, I cannot because this is indeed the case. I am not saying this is wrong, but that this argument is not valid; that's a logical fallacy, not a physical erroneous fact.

 

[Meir Achuz]

What argument is not valid?

 

[coquelicot]

What argument is not valid?

The following argument is not valid:

"The potentials on the conductors depend uniquely and linearly on the charge distributions on the surfaces of the conductor" IMPLIES The potential on the conductors depends uniquely and linearly on the net charge of the conductors. What is false is the "IMPLIES".
In mathematical form, assuming there are $n$ conductors $C_i$ with charge distribution $\rho_i$:
It is true that $V(C_i) = f(\rho_1, \rho_2, \ldots \rho_n)$, where $f$ is a 1-1 linear operator $(L^1)^n\to \mathbb R_+,$ because of the linearity of the Poisson equation and the uniqueness of its solution with Dirichlet or Neuman boundary conditions. BUT this does not imply a priori that
$$V(C_i) = g(\int_{C_1}\rho_1 dV, \ldots \int_{C_n}\rho_n dV)$$ for some linear 1-1 function $g$.
Indeed, there might exist a priori two different charge distributions $\rho_i$ and $\rho'_i$ that give rise the same net charges on the conductors. So, we would have
$$
V(C_i) = f(\rho_1, \ldots \rho_n)
= g(\int_{C_1}\rho_1 dV, \ldots \int_{C_n}\rho_n dV)
= g(\int_{C_1}\rho'_1 dV, \ldots \int_{C_n}\rho'_n dV)
= f(\rho'_1, \ldots, \rho'_n).$$
But this is impossible since $f$ is 1-1 and $(\rho_i)_i\ne (\rho'_i)_i$.
I did my best to explain the fallacy. Hopefully this is clear for you now.

 

[Meir Achuz]

Where in Jackson's (or some other textbook) Section 1.9 is this invalid argument used?

 

[coquelicot]

I don't have this book, but you can probably look at the section where he asserts the existence of the capacitance matrix (please, pay attention that the existence of the capacitance matrix between conductors is exactly the same as to say that the potentials of the conductors depends linearly on the net charge of the conductors). Then unless this book is different from many books I've read, you'll see a poor justification of the existence of the capacitance matrix. Otherwise, please, let me know his argument.

 

[Meir Achuz]

(or some other textbook)
My problem still is that the theorem you quote in your original post seems identical to the theorem proved in many EM textbooks. No textbook I know of permits specifying the Neumann boundary condition on a conductor.

 

[coquelicot]

(or some other textbook)

e.g, the excellent, famous, and deep book "Electrodynamics of continuous medias" by Landau and Lifshitz, chap 1 par. 2 p. 4. This is one among the many books, including Maxwell's one, that does not provide a real justification for the existence of the capacitance matrix.

My problem still is that the theorem you quote in your original post seems identical to the theorem proved in many EM textbooks. No textbook I know of permits specifying the Neumann boundary condition on a conductor.

Of course they do. The Neumann and Dirichlet boundary conditions are classic, and even dealt with in Wikipedia. But the condition on NET charge on the conductors is very different (apparently, it's difficult to grasp the differences between these concepts).
Concerning your doubts, unfortunately, you have not brought the exact statement of the theorem in the books you mentioned, nor their proof, nor even a reference online that I could check. So, I cannot answer you. If you wish, you can scan one page or two of their books and post it here. But without material, this discussion is going to nowhere.

 

[vanhees71]

I don't see what should be wrong with the derivation of the capacitance matrix in LL vol. VIII. It's a bit short, and maybe a little figure would be helpful, but I don't see a mistake.

 

[coquelicot]

I don't see what should be wrong with the derivation of the capacitance matrix in LL vol. VIII. It's a bit short, and maybe a little figure would be helpful, but I don't see a mistake.

LL ?

I may be unable to obtain some books in the short term. So, perhaps, a scan of the proofs you judge correct and complete would be welcome.

 

[vanhees71]

LL=Landau and Lifshitz. You quoted the book yourself. I thought you have access to it.

 

[coquelicot]

I don't see what should be wrong with the derivation of the capacitance matrix in LL vol. VIII. It's a bit short, and maybe a little figure would be helpful, but I don't see a mistake.

Assuming you refer to chap 1, par. 2, eq 2.2. The only thing I see is:

The charges and the potentials of the conductors cannot both be arbitrarily prescribed; there are certain relations between them; since the field equations in a vacuum are linear and homogeneous, these relations must also be linear, i.e. they must be given by equations of the form $$e_a = \sum_b C_{a,b} \phi_b.$$

So, you are perfectly right to say the the justification of the capacitance matrix is not incorrect: it is simply nonexistent. That's at most a "declaration of principle", but I don't see any proof here. But if you want to convince me that I'm wrong, you may try to write this declaration of principle in the form of mathematical formulae. The proof should begin with something like: according to Maxwell equations, we have $\nabla^2 V = etc.$ and ends with, hence $e_a = \sum_b C_{a,b} \phi_b.$
If you can do that, in say, 10 lines, without using the theorem in the question, I will happily call myself an idiot.

 

[coquelicot]

EDIT OF MY PREVIOUS POST: I was apparently tired yesterday night. The result $e_a = \sum_b C_{a,b} \phi_b$ is not the real problem, and can be deduced easily from the linearity (as claimed by the authors) and the uniqueness thm of the Laplace equation with Neuman boundary conditions. What is another story is to derive the inverse relation $\phi_b = \sum_a C_{a,b} e_a$ ( that is, the fact that the matrix $C_{a,b}$ is invertible).

This relation is simply asserted by the authors just below the cited paragraph, without any justification.

 

[renormalize]

It can be shown by energy considerations that the mutual-capacitance matrix of a collection of conductors must be symmetric. Moreover, its diagonal elements (the self-capacitance of the individual conductors) are all positive. Hence, the capacitance matrix is positive definite and therefore invertible. (Its inverse is called the elastance matrix.) See, e.g., these EE lecture notes from UC Berkeley: http://rfic.eecs.berkeley.edu/~niknejad/ee117/pdf/lecture11.pdf

 

[coquelicot]

It can be shown by energy considerations that the mutual-capacitance matrix of a collection of conductors must be symmetric. Moreover, its diagonal elements (the self-capacitance of the individual conductors) are all positive. Hence, the capacitance matrix is positive definite and therefore invertible. (Its inverse is called the elastance matrix.) See, e.g., these EE lecture notes from UC Berkeley: http://rfic.eecs.berkeley.edu/~niknejad/ee117/pdf/lecture11.pdf

Thank you for your answer. I was aware of the possibility to use the quadratic form defined by the capacitance matrix to show it is invertible, but the proof is still incomplete in my opinion. Please let me know what you think.
To begin with, I have two observations:

1. the fact that the diagonal elements of the cap matrix are all positive and the matrix is symmetric does not implies that it is positive definite: for example the matrix $\begin{pmatrix}1 & 1\\ 1 & 1\end{pmatrix}$ is not invertible (and hence not definite).

2. the presentation you joined is not a rigorous exposition, but a mix of theory with some "experimentation like arguments", whose truth is admitted implicitly without proof. For example: "Since conductor 2 is grounded, there is no energy required to add or remove charge from it." While I believe this assertion is true, this has to be mathematically formulated and proved. And this document contains many other things like this. Notice, by the way, that the existence of the capacitance matrix and its invertibility is admitted from the beginning of this document without proof.

So, I propose to you to take a very good and well formulated exposition available online to all of us, namely "Electrodynamics of continuous medias" by Landau and Lifshitz (just google it).
In P.5 of this book, we can find a perfect demonstration that the capacitance matrix is symmetric, and an almost perfect demonstration of the fact that the electrostatic energy stemming from the charges on the conductors is a quadratic form whose matrix is exactly the capacitance matrix.
Please, notice also that there is a fallacy sooner in the exposition of this book: the authors, at p. 4, eq. (2.4) assert without proof that the capacitance matrix is invertible, which is what we are trying to prove. Fortunately, this fact is not really needed in their derivation p. 5, so we may simply forget it.
Now, the argument could be elegant (albeit not trivial, as can be seen): since the energy must be always positive, and not null unless the potentials are null everywhere, the quadratic form must be definite and positive, that is, the cap matrix must be invertible.
This is fine, but there remains a problem in the demonstration (in my opinion): the fact that
$$ {\partial^2 U\over \partial \phi_a \partial \phi_b} = C_{a,b}$$ does not implies that
$$ U = {1\over 2} \sum _{a,b}C_{a,b}\phi_a \phi_b,$$ but that
$$U = {1\over 2} \sum _{a,b}C_{a,b}\phi_a \phi_b + f_{a,b}(\phi_a) + g_{a,b}(\phi_b), $$
with $f_{a,b}$ and $g_{a,b}$ arbitrary functions. I have no idea of how to overcome this problem.

Note: All of this is valid if the conductors are located in empty space. I'm not so sure this remains valid if dielectrics are surrounding the conductors. This is another possible problem.

 

[renormalize]

You are correct, my argument for the invertibility of the capacitance matrix in post #25 was incomplete. But as you also point out, Landau & Lifshitz (L&L) give a proper proof in "Electrodynamics of Continuous Media", so I think we are in agreement that this matrix is indeed invertible.
That said, I don't understand your objection to expressing the capacitance matrix as the second derivative of the electrostatic energy $U$ with respect to the potentials. After all, L&L state in their eq.(2.2) that
$U=\frac{1}{2}\sum_{a}e_{a}\phi_{a}$ , where $e_{a}$ are the charges and $\phi_{a}$ are the potentials on the conductors. Then in eq.(2.3) they linearly relate the charges to the potentials via the capacitance matrix, namely $e_{a}=\sum_{b}C_{ab}\phi_{b}$ . Combining these expressions gives precisely $U=\frac{1}{2}\sum_{a}\sum_{b}C_{ab}\phi_{b}\phi_{a}$ with no "arbitrary functions" appearing anywhere. So where is the problem?

 

[coquelicot]

You are correct, my argument for the invertibility of the capacitance matrix in post #5 was incomplete. But as you also point out, Landau & Lifshitz (L&L) give a proper proof in "Electrodynamics of Continuous Media", so I think we are in agreement that this matrix is indeed invertible.
That said, I don't understand your objection to expressing the capacitance matrix as the second derivative of the electrostatic energy $U$ with respect to the potentials. After all, L&L state in their eq.(2.2) that
$U=\frac{1}{2}\sum_{a}e_{a}\phi_{a}$ , where $e_{a}$ are the charges and $\phi_{a}$ are the potentials on the conductors. Then in eq.(2.3) they linearly relate the charges to the potentials via the capacitance matrix, namely $e_{a}=\sum_{b}C_{ab}\phi_{b}$ . Combining these expressions gives precisely $U=\frac{1}{2}\sum_{a}\sum_{b}C_{ab}\phi_{b}\phi_{a}$ with no "arbitrary functions" appearing anywhere. So where is the problem?

Perfect! and thank you. There remains a small shadow: following the derivation of LL, it seems that all of this is valid whenever the conductors lie in free space, where we have $\Delta V = 0$, but not if they lie inside dielectrics (apparently), unless the demonstration could be adapted.