mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
If a particle of mass $m$ has velocity $v$, its momentum is $p=mv$.
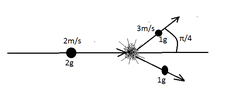
In a game with balls, one ball of mass $2g$ springs with velocity $2m/s$, it hits two balls, both of which have mass $1g$, and stops.
The one ball get soared with velocity $3m/s$ and with angle $45^{\circ}$ to the direction that has the biggest ball at the moment of the crash, as is shown below.
View attachment 5342
Supposing that the total momentum is the same before and after the crash, I have to find with what angle and velocity the second ball will move.
I have done the following:
Let $(u,v)$ be the unit vector in the direction of the desired velocity.
Let $\theta$ is the desired angle. $(1,0)$ is the unit vector of the $x$-axis.
Then we have that $(u,v)\cdot (1,0)=\cos\theta \Rightarrow u=\cos\theta$.
Since the vector is unit, we have that $u^2+v^2=1 \Rightarrow v^2=1-u^2 \Rightarrow v^2=1-\cos^2\theta \Rightarrow v^2=\sin^2\theta \Rightarrow v=\pm \sin\theta$.
Since the desired vector shows to the negative $y$, we reject $v\sin \theta$, or not?
So, the unit vector is $(u,v)=(\cos \theta , -\sin \theta)$.
Therefore, the velocity vector that we are looking for is $v_2(\cos \theta , -\sin \theta)$, where $v_2$ is the magnitude of the velocity.
From the Momentum Conservation Principle at the $x$-axis we have the following:
$$4=3\cos \frac{\pi}{4}+v_2\cos\theta \Rightarrow v_2\cos\theta=4-3\frac{\sqrt{2}}{2} \tag 1$$
From the Momentum Conservation Principle at the $y$-axis we have the following:
$$0=3\sin \frac{\pi}{4}-v_2\sin\theta \Rightarrow v_2\sin\theta=3\frac{\sqrt{2}}{2} \tag 2$$
Therefore, $$v_2^2\cos^2\theta+v_2^2\sin^2\theta=16-12\sqrt{2}+\frac{9}{2}+\frac{9}{2}=25-12\sqrt{2} \Rightarrow v_2^2=25-12\sqrt{2} \\ \Rightarrow v_2=\pm \sqrt{25-12\sqrt{2}}$$
Is this correct so far? (Wondering)
If a particle of mass $m$ has velocity $v$, its momentum is $p=mv$.
In a game with balls, one ball of mass $2g$ springs with velocity $2m/s$, it hits two balls, both of which have mass $1g$, and stops.
The one ball get soared with velocity $3m/s$ and with angle $45^{\circ}$ to the direction that has the biggest ball at the moment of the crash, as is shown below.
View attachment 5342
Supposing that the total momentum is the same before and after the crash, I have to find with what angle and velocity the second ball will move.
I have done the following:
Let $(u,v)$ be the unit vector in the direction of the desired velocity.
Let $\theta$ is the desired angle. $(1,0)$ is the unit vector of the $x$-axis.
Then we have that $(u,v)\cdot (1,0)=\cos\theta \Rightarrow u=\cos\theta$.
Since the vector is unit, we have that $u^2+v^2=1 \Rightarrow v^2=1-u^2 \Rightarrow v^2=1-\cos^2\theta \Rightarrow v^2=\sin^2\theta \Rightarrow v=\pm \sin\theta$.
Since the desired vector shows to the negative $y$, we reject $v\sin \theta$, or not?
So, the unit vector is $(u,v)=(\cos \theta , -\sin \theta)$.
Therefore, the velocity vector that we are looking for is $v_2(\cos \theta , -\sin \theta)$, where $v_2$ is the magnitude of the velocity.
From the Momentum Conservation Principle at the $x$-axis we have the following:
$$4=3\cos \frac{\pi}{4}+v_2\cos\theta \Rightarrow v_2\cos\theta=4-3\frac{\sqrt{2}}{2} \tag 1$$
From the Momentum Conservation Principle at the $y$-axis we have the following:
$$0=3\sin \frac{\pi}{4}-v_2\sin\theta \Rightarrow v_2\sin\theta=3\frac{\sqrt{2}}{2} \tag 2$$
Therefore, $$v_2^2\cos^2\theta+v_2^2\sin^2\theta=16-12\sqrt{2}+\frac{9}{2}+\frac{9}{2}=25-12\sqrt{2} \Rightarrow v_2^2=25-12\sqrt{2} \\ \Rightarrow v_2=\pm \sqrt{25-12\sqrt{2}}$$
Is this correct so far? (Wondering)
Attachments
Last edited by a moderator: