SUMMARY
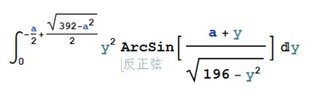
The integral $$\int_{0}^{\frac{-a}{2}+\frac{\sqrt{392-{a}^{2}}}{2}} {y}^{2}\arcsin\left({\frac{a+y}{\sqrt{196-{y}^{2}}}}\right)\,dy$$ can be evaluated numerically using GNU Octave and PTC Mathcad Prime 3.0. In GNU Octave, the function is defined as f = @(a, y) y^2 * asin((a + y) / (sqrt(196 - y^2))), and numerical integration is performed using the quad function. Users can visualize the results with the plot function, while PTC Mathcad Prime 3.0 allows for straightforward algebraic interpretation of the integral.
PREREQUISITES
- Familiarity with numerical integration techniques
- Basic understanding of the arcsine function
- Experience with GNU Octave or PTC Mathcad Prime 3.0
- Knowledge of function plotting in programming environments
NEXT STEPS
- Explore advanced numerical integration methods in GNU Octave
- Learn how to use PTC Mathcad Prime 3.0 for symbolic computation
- Investigate the properties of the arcsine function and its applications
- Study function visualization techniques in Octave and similar software
USEFUL FOR
Mathematicians, engineers, and students interested in numerical methods and software tools for evaluating complex integrals.