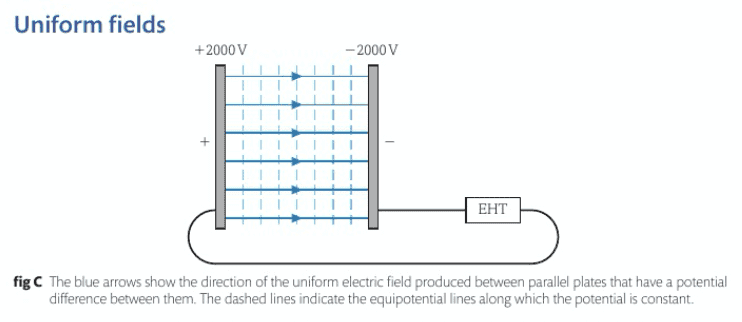
SUMMARY
The discussion clarifies why field lines are parallel in a uniform electric field created by charged plates. It emphasizes that the charges on the plates generate radial fields, which individually do not exhibit parallel lines. However, the vector sum of these radial fields results in a uniform field with parallel lines, particularly due to the perpendicular nature of the resultant fields at the surface of the plates. The analogy with wave propagation, specifically Huygens' principle, illustrates how adjacent sources can create a linear wave front.
PREREQUISITES
- Understanding of electric fields and charge distribution
- Familiarity with vector summation in physics
- Knowledge of Huygens' principle in wave theory
- Basic concepts of radial fields and their properties
NEXT STEPS
- Research "Vector addition of electric fields" to understand how fields combine
- Study "Huygens' principle" for insights into wave propagation
- Explore "Electric field lines and their properties" for deeper comprehension
- Investigate "Uniform electric fields in capacitor design" for practical applications
USEFUL FOR
Students of physics, educators explaining electric fields, and engineers involved in designing capacitors or related electrical components.