Why Are My Reactions Not Symmetrical?

[6Stang7]

I have a fixed-end fixed-end beam with two roller supports as well and a load applied in the center of the beam, as shown below.

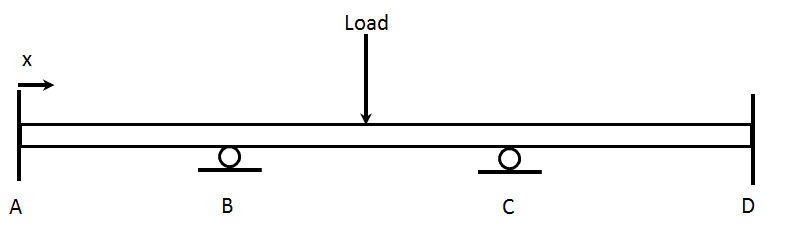
I've chosen my redundant forces to be the force at B (point up), the force at C (pointing up), the force at D (pointing up) and the moment at D (counter-clockwise).

I'm solving for these reactions using deflection and slope equations for a cantilever beam; specifically:

The sum of all the redundant force and the applied load will produce a net deflection at B=0
The sum of all the redundant force and the applied load will produce a net deflection at C=0
The sum of all the redundant force and the applied load will produce a net deflection at D=0
The sum of all the redundant force and the applied load will produce a net slope at D=0

using these equations: http://www.advancepipeliner.com/Resources/Others/Beams/Beam_Deflection_Formulae.pdf

I wrote up a worksheet in MathCAD and used matrix inversion to solve for the redundant forces. However, I am highly suspicious of the answers because the reactionary forces at B and C are not the same (as I'd assume they would be due to symmetry). Here is my worksheet:

Anyone see any errors that I have made?

 

[gsal]

What happened to the force and momentum at A? I understand that they should be the same as at D? You basically have a symmetric problem here.

 

[6Stang7]

What happened to the force and momentum at A? I understand that they should be the same as at D? You basically have a symmetric problem here.

The force and moment at A doesn't factor into this (just yet at least). The compatibility equations are used to solve for the redundant forces.

See here for a detailed explanation: http://www.sut.ac.th/engineering/civil/courseonline/430331/pdf/09_Indeterminate.pdf

 

[SteamKing]

An inspection of your A matrix shows that it is symmetric about the main diagonal except for A(1,2) and A(2,1).

On a numerical analysis note, since the beam is composed of the same material throughout and the I of each segment is the same, the quantity EI can be set to 1 without affecting the C vector.

 

[6Stang7]

An inspection of your A matrix shows that it is symmetric about the main diagonal except for A(1,2) and A(2,1).

Ack! Good catch! I wrote the wrong equation for A(1,2) ; checking the general formula gives an equation that is the same as A(2,1) (as you pointed out). Making this adjustment gives me symmetric results that make sense.

On a numerical analysis note, since the beam is composed of the same material throughout and the I of each segment is the same, the quantity EI can be set to 1 without affecting the C vector.

Very good point; the E*I can be factored out of both matrices.