Discussion Overview
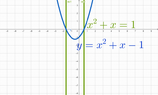
The discussion revolves around the equation x² + x = 1 and the emergence of the values (-1.618, 0) and (0.618, 0) as solutions. Participants explore the implications of these solutions, their graphical representation, and connections to concepts such as the Fibonacci sequence and the golden ratio. The conversation includes both algebraic reasoning and graphical interpretations.
Discussion Character
- Exploratory
- Technical explanation
- Conceptual clarification
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant asks for clarification on why the values (-1.618, 0) and (0.618, 0) emerge from the equation x² + x = 1.
- Another participant suggests that the values are solutions to the equation and proposes plotting the graph of y = x² + x - 1 instead.
- Some participants discuss the relationship between the solutions and the golden ratio, noting that the polynomial x² + x - 1 is related to Fibonacci sequences.
- There is mention of using the quadratic formula to find the roots of the equation, which yields the values in question.
- Several participants express confusion about the nature of the graph, with some noting that the equation x² + x = 1 represents two points rather than a continuous curve.
- One participant raises a question about the applicability of the quadratic formula to other types of equations, such as cubic equations.
- There is a discussion about the need for additional techniques when analyzing equations and their graphs, particularly in relation to intersections and asymptotic behavior.
Areas of Agreement / Disagreement
Participants generally agree that the values (-1.618, 0) and (0.618, 0) are solutions to the equation, but there is disagreement and confusion regarding the graphical representation and the implications of these solutions. The discussion remains unresolved regarding the broader connections to other equations and methods of solving them.
Contextual Notes
Participants express uncertainty about the graphical interpretation of the equation and the relationship between different types of equations. There are also limitations in understanding how to transition between equations and their graphical representations.