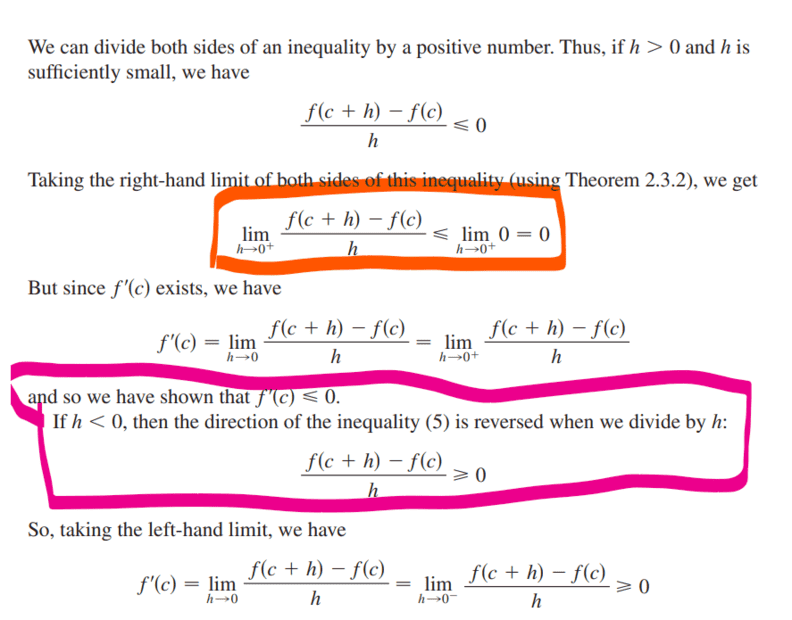SUMMARY
This discussion clarifies the mathematical principle that allows limits to be taken on both sides of an equation or inequality. When two expressions are equal, their limits will also be equal, which is essential in calculus, particularly in the limit definition of the derivative. The conversation highlights the importance of ensuring that the variable in the denominator, such as h, is positive to maintain the direction of inequalities during limit calculations. The final conclusion drawn is that if the limits exist, they can be equal, reinforcing the validity of the limit process in calculus.
PREREQUISITES
- Understanding of limits in calculus
- Familiarity with the limit definition of the derivative
- Knowledge of inequalities and their properties
- Basic algebraic manipulation skills
NEXT STEPS
- Study the limit definition of the derivative in detail
- Explore the properties of limits involving inequalities
- Learn about the epsilon-delta definition of limits
- Investigate examples of limits approaching boundaries in calculus
USEFUL FOR
Students of calculus, mathematics educators, and anyone looking to deepen their understanding of limits and derivatives in mathematical analysis.