Salmone
- 101
- 13
In a Michelson interferometer with a monochromatic laser, why do we always see an interference pattern even if we move one of the mirrors?
Shouldn't it be a certain distance for which the movable mirror reflects the wave to be in opposite phase with the other wave so that they interfere destructively and we do not see anything on the screen?
Instead, I see in some videos that we always see an interference pattern and the only effect one see when moving the mirror is a change in this pattern but we still see light.
Shouldn't the movable mirror give in a certain position the same situation as the image?
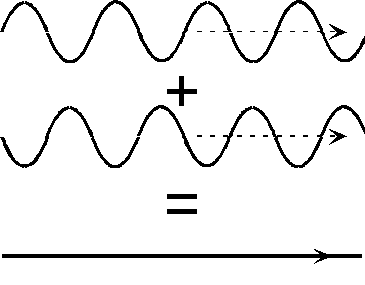
Shouldn't it be a certain distance for which the movable mirror reflects the wave to be in opposite phase with the other wave so that they interfere destructively and we do not see anything on the screen?
Instead, I see in some videos that we always see an interference pattern and the only effect one see when moving the mirror is a change in this pattern but we still see light.
Shouldn't the movable mirror give in a certain position the same situation as the image?