- #1
musicgold
- 304
- 19
Homework Statement: This is not a homework question.
I am trying to understand why we spend so much time studying trig identities.
Homework Equations: As far as I understand, the two basic trig functions (sin and cos ) show the relationship between the sides of a right angle triangle in a unit circle. We care about them because we can apply this knowledge in many engineering and physics situations.
What I don't get is why we care so much about identities like
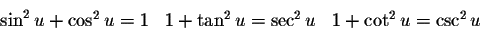 .
.
Why should I spend time learning and remembering something like ## cos u . sin v = \frac {1}{ 2} [sin(u + v) − sin(u − v)] ##
Here is how I tried to understand ## (sin u + cos v )^2 = sin^2 u +cos^2 v + 2 sin u . cos v ## . All I see is sinusoidal functions with different periods and some of them are always positive.
How do I use this knowledge?
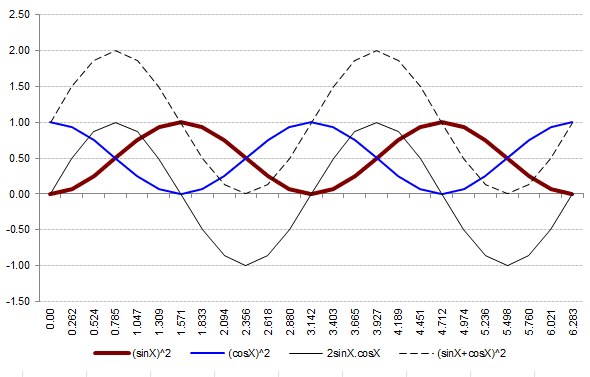
I am trying to understand why we spend so much time studying trig identities.
Homework Equations: As far as I understand, the two basic trig functions (sin and cos ) show the relationship between the sides of a right angle triangle in a unit circle. We care about them because we can apply this knowledge in many engineering and physics situations.
What I don't get is why we care so much about identities like
Why should I spend time learning and remembering something like ## cos u . sin v = \frac {1}{ 2} [sin(u + v) − sin(u − v)] ##
Here is how I tried to understand ## (sin u + cos v )^2 = sin^2 u +cos^2 v + 2 sin u . cos v ## . All I see is sinusoidal functions with different periods and some of them are always positive.
How do I use this knowledge?