Why does a coil squash my function generator signal?

[Albertgauss]

Greetings,

In the first picture below, I create a 5 volts sine amplitude signal with a frequency of about 100 Hertz. The 3 Ohm, 400 turn coil (that will eventually be part of a transformer) is not initially connected. The output waveform from my function generator completely matches my input waveform to Channel of my scope. No problem there. However, if you look at my next picture, when I try to apply my waveform across my coil, it completely squashes my signal! Is this supposed to happen? Why does this happen? My signal goes from 5 volt amplitude to about 50 millivolts (easier to see in person but you can see in the photo this is about so--I left the vols/div knob at 5 volts to compare). It seems to me that my waveform should still be 5 volt amplitude. The frequency remained unchanged whether I connected or disconnected the coil.

 

[rbelli1]

What is the output impedance of the generator? What is the impedance of the coil at 100Hz? Have you tried any other frequencies?

BoB

 

[Albertgauss]

The function generator is on its "High Z" setting. What I could find from this model (Tektonix AFG 1022) is that "High Z" means some output impedance above 10,000 Ohm (10kOhm) but I couldn't find the exact value. Is the "High Z" output impedance something standardized between off-the-shelf generators or does each function generator have its own "High Z" value? In regards to other frequencies, the coil squashed the waveform in the range up to 10 kiloHertz or so. I will double-check that tomorrow, but I do remember trying other frequencies and getting the same squashed signal. Could the o-scope be reacting to the coil? I hadn't thought of that until now. If the O-scope is somehow the culprit, what should I look for about it that could cause this behavior?

 

[Baluncore]

If there is conductive material near the coil, such as in the table top, then the materialt will act like a shorted turn. To test for local metal, turn the coil on it's side and see if it changes the response.

The coil is an inductor with low series resistance. What is the inductance, L ?
The reactance of the coil will be XL = 2 * Pi * L.
You are driving that reactance through a Hi-Z series output impedance, so expect a potential divider effect.

Can you set the generator to a 50 ohm series output impedance?
Can you set the oscilloscope to a 50 ohm parallel input impedance?
Do you under stand what thet means?

 

[Albertgauss]

I will check the tabletop. It doesn't seem like there was any contact between any metal or conductive part of the coil or alligator clips, but it is easy enough to move to another surface. This will be easy to check today. In fact, maybe it is possible the yellow housing of my coil is some conductive material I hadn't considered before.

I didn't think to calculate the inductance of the coil but I will today also. I am thinking that with 400 turns, a few centimeters in length, and about a 1 cm in radius, the inductance will be on the order of tens of milliHenris, my guess is about 50 mH. I realize that at 100 Hertz, I am getting about 30 Ohms of impedance of the coil, with large errors bars. I will have more precise numbers in a few hours.

When I had the 50 Ohm output impedance on the function generator selected and the coil was unconnected, I was getting twice the signal on my oscope. I read about this effect after that. The easiest choice seemed to be to switch to the High Z output impedance choice on the function generator, since I do not have a 50 Ohm terminator handy. Not hard to get, but since I have to order/buy one, that will take some time. However, I did not know that the oscope most likely will have a 50 Ohm input impedance I can use to terminate the 50 Ohm output impedance of the function generator. I will try that in a few hours. That would be the easiest fix of everything. I will let you know what I find.

 

[Baluncore]

It doesn't seem like there was any contact between any metal or conductive part of the coil or alligator clips, but it is easy enough to move to another surface.

I am not suggesting conductive contact with the clips or wires. I am suggesting that with a vertical axis coil, a metallic conductor below the coil, such as the bench frame, or under the bench cover, would intercept the flux and a large eddy current would flow. The conductive sheet would appear as a single shorted turn secondary winding.
The coil bobbin is most unlikely to be conductive.

 

[Rive]

You should try making an estimation about the impedance of the coil at the frequency you are using. A serial resistor might help.

Try it with higher frequencies and also you can try it with some core inside the coil (the core should be something what is designed as transformer core at the actual frequency).

 

[AshTown]

With the function generator in "Hi Z" mode, it is like the function generator has a 100,000 ohm resistor in series with its output. When it feeds a 4 ohm coil, the voltage across the coil will be 4/100004 * 5 Volts.

 

[Albertgauss]

Okay, I did more tests.

First, in regards to their metal under the bench (bench frame/bench cover) etc, that did not seem to be the problem. I put the coil on fur, plastic, etc and the behavior did not change. So we can rule out a conductor beneath the coil from the surface tabletop upon which I am using. It could have been a possibility, though, unknown until I tested for that, and there have been far stranger things to create strange voltages in other circuits I have worked with.

The inductance of that coil is, for 400 turns, 2 cm width, 4 cm height, wire diameter 0.1 millimeter, rectangular and hollow, 21.2 milliHenries. This from the site: https://www.eeweb.com/tools/rectangle-loop-inductance

Also, the oscope channel 1 input imedance is 1 MegaOhm in parallel with a 20 picoFarad Capacitor.

I think the voltage divider phenom that you are all talking about is the reason to why the current got squashed. The 400 turn coil has an impedance of, at 100 Hertz, 13 Ohms. At 10,000 Hertz, the impedance becomes 1319 Ohms. It appears I did not test for as high a frequency as I initially wrote, because I redid the tests today and around 8,000 Ohms, the signal on the scope matched the signal of the function generator. From 100 Hz to 7000 Hz, the waveform on the scope gradually approached the waveform on the generator. After 7000 Hz, the waveform on the scope and function generator matched, all the way up to 1 MegaHertz. As long as I stay above 7,000 Hz, then my FG wave will be put across the coil unchanged.

But the numbers of AshTown don't seem quite right. If the output impedance of the function generator is 100,000 Ohms, and I am at 10,000 Hertz that would give me 5 volts*1319/(100,000 + 1319) = 65 millivolt. I clearly measured 5 volts though. If I assume the function generator output impedance is 10,000 Ohm, I get 5 volts*1319/(100,00 + 1319) = 0.6 volts, still a factor of 10 too small. However, if I assume a 50 Ohm function generator output impedance, I get: 5 volts*1319/(50 + 1319) = 4.8 volts, which, now as I do this, seems quite coincidental.

I'm pretty sure I was on the High Z output impedance and not the 50 Ohm--except that my data suggests the opposite. I don't remember switching back to the 50 Ohm output impedance. I did think I checked my settings. Its only as I type this now that I realize I may have been on 50 Ohm setting today when I did these tests. Sigh, I will confirm that tomorrow to tell one way or the other.

I will also try the core tomorrow. All of these tests had it out--just using the coil open air. This is my first chance to see the new emails today because I can't get to gmail at work, and have to wait until I get home to see the replies.

 

[Baluncore]

I put the coil on fur, plastic, etc and the behavior did not change. So we can rule out a conductor beneath the coil from the surface tabletop upon which I am using.

Magnetic fields are not affected by fur or plastic so I would not have expected it to change. You must turn the coil on it's side to change the magnetic flux orientation relative to the bench top. You have not yet ruled anything out.

In high impedance output mode, the function generator will output the specified voltage from it's output driver. It will be able to supply several mA.
In 50 ohm output mode, the sig-gen will have a 50 ohm termination resistor in series with it's output. It will provide twice the specified voltage to the resistor, which will be attenuated to half by the 50 ohm external load, to give the indicated voltage.
The same driver may be used in both cases, only the voltage display is changed by a factor of two.

 

[Asymptotic]

Found this video that may prove helpful, but doesn't address what happens when driving signal into a low impedance.

The 400 turn coil has an impedance of, at 100 Hertz, 13 Ohms.

How much current does 13 ohms of load demand at 5 V p-p?
Can this function generator deliver that much current?
If no, what does this particular generator do when overloaded?

 

[Albertgauss]

ok. I read everything. I will try the new suggestions today. I'll let you know what I find out this evening.

 

[AshTown]

If you connect only an oscilloscope, no coil, to the function generator when it is set to "high Z" (100,000 ohms) mode and 5V output
and
the input impedance of the the oscilloscope is 10,000,000 ohms, say,
then
the signal at the oscilloscope will be 10,000,000/10,100,000*5V i.e. about 5V
As you can see, it is the low impedance of the coil that attenuates the signal so severely.

 

[Albertgauss]

The first picture below, setup.jpg, shows my circuit. The waveforms coming out of the function generator are identical in freq and voltage for each jpeg on this reply. The output voltage from both function generator output channels are always 1 volt amplitude (I changed from 5 volts to 1 volt to make study easier). The coils are the same also, each with an inductance of 0.0212 Henry. The Channel 1 function generator is on the “High Z” impedance output and function generator Channel 2 is on the 50-Ohm Impedance output---this is what "High Z" and "50 Ohm" mean where marked on all he jpegs I attached to this reply.

In the setup, hopefully there is no interference with any other flux except what the coils themselves produce. The coils are elevated on styrofoam. I did try the coils to be horizontal and vertical, with no change in signal.

In regards to what “High Z” means numerically, the user manual had this to say: "Selectable: 50 Ω, 1 Ω to 10.000 kΩ, High Z (adjusts displayed amplitude according to selected load impedance)"

(The website is https://www.tek.com/datasheet/arbitrary-function-generator)

I don’t know what it means that “according to selected load impedance”. Does the Function Generator somehow sense what impedance is in my circuit and then adjusts its output impedance to match, for cases of “High Z”? Seems unlikely a function generator can do this, but I'm not sure.

Some data:

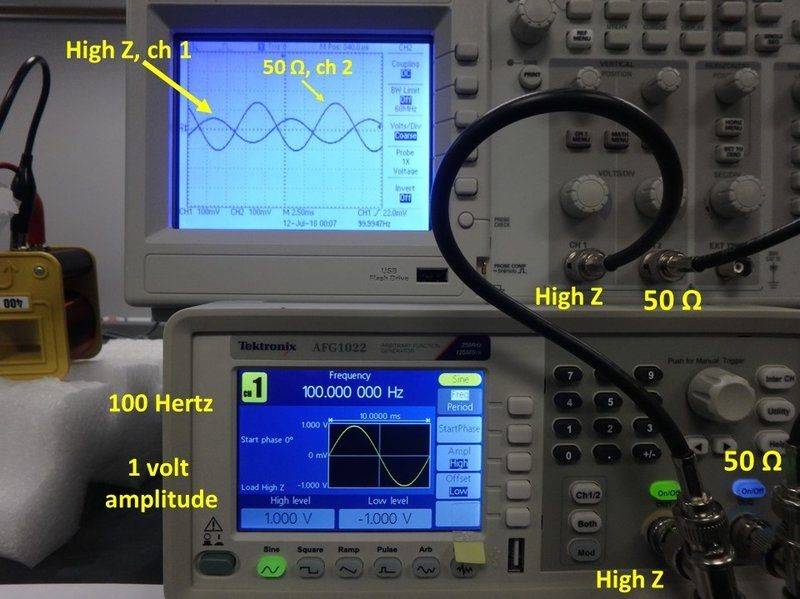
In the jpeg, 100Hz.jpg below, both channels are driven at 100 Hertz so the impedance of each coils is 13.2 Ohms. The 50-Ohm FC output impedance should give a voltage of 13/(13+50) = 0.21 volts on the oscope display, but you can see from "50 Ohm, ch2" on the jpeg below that this calculation disagrees with the 0.12 volts that is actually there. The voltages divisions on both oscope channels are 100 millivolts per division. The High Z output function generator impedance gave on the scope a voltage of 80 millivolt, (High Z, ch 1) but if you calculate what the voltage should be on the oscope screen assuming High Z = 10,000 Ohms, you get 13/(13+10,000) = 1 millivolt, far different than the 80 millivolts measured below.

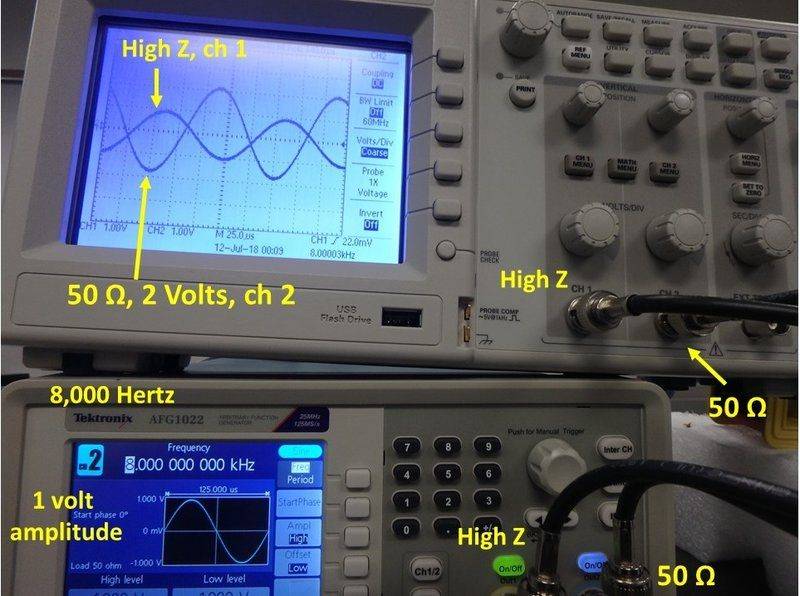
In the jpeg below, 8000 Hz, each channels is driven at 8000 Hertz so the impedance of each coil is 1065 Ohms. The 50-Ohm FC output impedance should give a voltage of 1065/(1065+50) = 0.95 volts on the oscope display, but you can see below that this calculation disagrees with the nearly 2.0 volts that is actually there (50 Ohms, 2 Volts, ch 2). The High Z output function generator impedance gave on the scope, assuming again a High Z of 10,000 Ohms, 1065/(1065+10,000) = 0.09 volt, but the scope clearly shows a display of 1 volt (High Z, ch 1), or, exactly what is coming out of the function generator. The vertical volts/div are now 1.00 volts for both oscope channels. Thus, the High Z cannot be 10,000 Ohms. This is not a problem for me, because I know that for this kind of circuit, as long as I run it at 8,000 Hertz or higher, what I output from the function generator will be, indeed, what is fed to my circuit.

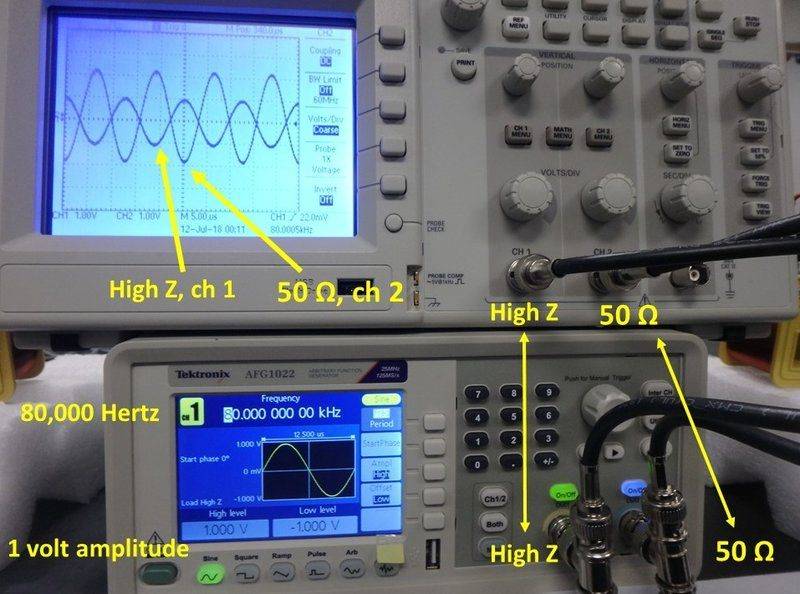
The jpeg 80000Hz.jpg below has the same story as the jpeg 8000 Hz. Each channels is driven at 80,000 Hertz so the impedance of each coil is 10,656 Ohms. The 50-Ohm FC output impedance should give a voltage of 10656/(10656+50) = 0.99 volts on the oscope display, but you can see below that this calculation disagrees with the nearly 2.0 volts that is actually there (50 Ohms, ch 2). The vertical volts per division is again 1.00 volts for both channels on the oscope. The High Z output channel, however, gave the same waveform on the scope as the function generator, though at some other function generator output of 10,000 or 100,000 Ohms (which both predict the wrong oscope display). At 80,000 Hertz, the High Z will be the function generator output impedance option selected for my circuit.

In regards to Asymptotic, I could not find the max currents from the usual datasheet. I contacted tech support at Textronix and they could not find this information immediately, but promised to send me an email when they do so. Its obviously a good point, though, and I will report here what they tell me. 13 Ohms at 5 volts expects, from Ohm’s Law, a current of 0.38 Amps. A DC power supply could put this out, no problem, but it remains to be seen whether a function generator of the tabletop class I am using can do that AC.

For Ashtown, let me if I understand what you wrote in your last reply.

No coil means a load on the oscope input of R_s = 1,000,000 Ohms, R_fg = 100,000 Ohms so that 1,000,000/(1,000,000+100,000) ~ V_disp = V_fg

With Coil at 100 Hz as load R_c = 13 Ohms, R_fg = 100,000 Ohms, 13/(13+100,000) ~ (0.0001)*V_disp << V_fg hence, a squashed signal and is what is meant when you said the low impedance is responsible for squashing the signal. Where does the oscope impedance go in this calc though? Why is it not considered anymore?

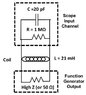
Finally, the last jpeg, schematic.jpg. Do I have this schematic correct for the circuit I am working on? No one has mentioned the 20 pF capacitor. When is it important? I know that the impedance of a capacitor is 1/(omega*capacitance). As some frequencies of my circuit, it did have impedances on the order of other impedances in my circuit, but the cap did not seem to have any effect. How come?

 

[CWatters]

50R and 10k are reasonably standard load impedances which is why your signak generator provides them as options.

 

[CWatters]

The attenuation (squashing) you are seeing is due to the potential divider effect previously mentioned. The power transferred from source to load is a maximum when source and load impedances match. Eg both 50R or both 10k etc. You should prove this to yourself by looking at how power dissipated in a potential divider circuit.

I should point out that a signal generator doesn't usually have a power amplifier built in. Eg They aren't usually designed to drive very low impedances loads like 4R speakers. The 50R setting is designed to drive 50R coaxial cable. The 10kohm setting is designed to drive things like audio amplifiers that might have a 10kohm input impedance.

 

[CWatters]

At 80khz the impedance of a 21mH inductor will be about...

=2pi*80,000*21*10^-3
=2pi*80*21
=10,000

The 20pf input capacitance of the scope is in parallel with the inductor. Work out the impedance of the capacitor and see how it compares with the 10k impedance of the inductor. Is it much smaller or much bigger?

 

[Tom.G]

The approximate factor of two disagreement between calculations and readings is due to ignoring the 50Ω input and output impedances of the test equipment. For instance with the both the generator and 'scope set at 50Ω you have 2-to-1 divider; 50Ω generator impedance and a 50Ω 'scope load. For the frequencies you are usning, I recommend you set the 'scope for high input impedance.

The remaining discrepancies, if below 10%, are likely just experimental errors due to instrument calibrations, limited screen reading resolution, and uncertainty about the exact coil values.

Cheers,
Tom

 

[CWatters]

Good catch.

 

[Albertgauss]

Last bit, got busy, but I did have a few more comments.

I didn't realize 50 Ohm and 10k were standard, that a lot of equipment is designed this way. That does make sense though, especially with BNC cables as they are at 50 Ohms or so.

I did prove myself that the Power is a max when the impedances match. Let R_L is the load resistance, I_L the current flowing through the load and V_source the input voltage, and P_L be the power dissipated by the load resistor. This calc is P_L =[(I_L)^2]R_L and then the current through the load, R_L is V_source = (R_L + R_S). Plug I_L into P_L expression, keep R_S constant (resistance of the source), take the derivative of P_L with respect to R_L and solve for R_L. You do, indeed, find that R_L maximizes P_L when it is equal to R_S.

With the impedance of the Cap, Z = 1/(2*Pi*f*C) and you get, for 80,000 Hertz, 100 kOhm for a capacitance of 20pF. This is a lot bigger than the impedance on the inductor at the same frequency. I see why it won't matter much for what I am doing here.

The high impedance setting, is, indeed, best for what I am doing.

Ok, I think I'm all good. I guess the hard part was understanding the electronics inside the scope and FG, but this has all been very useful to me. It was worth it to work through all this in detail. Unless there is anything else I forgot to answer or didn't get right, I thank everyone for their help.

 

[CWatters]

With the impedance of the Cap, Z = 1/(2*Pi*f*C) and you get, for 80,000 Hertz, 100 kOhm for a capacitance of 20pF. This is a lot bigger than the impedance on the inductor at the same frequency. I see why it won't matter much for what I am doing here.

Yes. You asked why the capacitance can be ignored...

If you have a very high impedance in parallel with a very low one the combintion has a very low impedance. So the effect of the large impedance can usually be ignored.

 

[CWatters]

In some cases the capacitance of the scope and the wire from your circuit to the scope does matter. You should look at how a x10 prob can help.

Edit: sorry I accidentally posted a draft of this. The submit button is too close on this tablet.

 

[Baluncore]

Take a look deep into the operators manual for that sig-gen. It seems it can adjust the Hi-Z output voltage, or the display, to compensate for the load on the Hi-Z output.

 

[Asymptotic]

I could not find the max currents from the usual datasheet. I contacted tech support at Textronix and they could not find this information immediately, but promised to send me an email when they do so. Its obviously a good point, though, and I will report here what they tell me. 13 Ohms at 5 volts expects, from Ohm’s Law, a current of 0.38 Amps.

You can gain a sense of maximum output current by connecting a DC ammeter to the function generator output. It will appear to the generator as nearly a short circuit (it depends on the meter manufacturer and range selected).

An amplifier can be used to drive heavy loads - Tegam, Accel Instruments, and others make them for this purpose - and here's a detailed DYI approach I chanced upon.

 

[Albertgauss]

Hi all,

Just to follow up, the manufacturer It will not be able to deliver that much current. Here is the conversation:

Your Request

Agent: Hello. How may I help you?
Me: ok. You still there?
Me: A question came up about the function generator afg 1022. I have an inductor that has 13 Ohms resistance when I drive a 100 Hertz Sine wave at 5 volts across it. The current should be 0.38 Amps. Can this function generator put out that much current? If not, what is the max current I can expect this function generator to put out? Is there a datasheet showing max current outputs at frequencies for this function generator?
Agent: Let me check
Me: ok
Me: Its okay if it can't put that current, but I would like to know what the max current output is for a combination of voltages and impedances
Me: Even if just ballpark combinations
Agent: Aright, let me see the user manual
Agent: -5 V to +5 V, 50 Ω load, -10 V to + 10 V, open circuit or high Z load
Agent: Still looking for the current spec
Me: Yes. I knew the above. Its the max current I can't find. I understand the max current output depends on impedance.
Agent: I can't seam to find it in the manual or the datasheet. I can do more digging and email you if I find something
Me: That would be best.
Me: Its okay if you need some time to do so. It doesn't seem to be easy specs to find
Agent: Sounds good. I appreciate your understanding
Agent: Take care
Me: ok

The manufacter replied:

"The basic setup of the generator is a voltage source in series with a 50 ohm resistor then your load. So you are not able to get a full 5 V out.
You will get about 2 V."

Anyway, that was a follow-up to when we asked about what the max current for 50 Ohm that this function generator could produce. Thanks for the advice about the 10X probe and Asymptotic's advice about the DC ammeter. Those are good ideas to try out.

 

[Chris Riccard]

http://www.sweethaven.com/sweethaven/ModElec/acee/frm0702.htm
the inductor is acting as filter squashing the signal because of the impendance of the circuit.

current is only limited by the 50 ohm and thou I don't remember much on sources and sinks a 10x probe shouldn't make a diff.