Generating a rising staircase waveform using an integrator?

[JC2000]

Summary:: My understanding of integrators and the waveforms they generate is hazy.

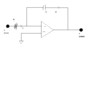
The question I am trying to solve is : Sketch the output waveform for an inverting integrator if the input signal is a square wave with amplitude 5 V and frequency 1kHz where the product of Resistance and Capacitance is 1.

I have the following questions with regard to the question, integrators and the waveforms they generate.



1. I have derived the equation relating input and output voltages however I am unable to understand exactly how the current is flowing, how the capacitor is behaving etc within the circuit...

2. I believe that the result is a triangular waveform output. However I don't really understand why :
a. What function do you integrate for a square waveform?
b. What is happening physically within the circuit to cause such an output?

3. Under what conditions does a square waveform input result for the same circuit result in the following output waveforms (if at all) :
a. An increasing staircase waveform (upto saturation)
b. An inverted triangular waveform
c. decreasing staircase waveform

(Regarding Q3. I believe that these outputs have something to do with the time period you consider during integration but I am unsure about why or how this would happen)

Thank you for your time!

 

[Averagesupernova]

You seem to be biting off a lot in one post. I will first tell you that a constant current through a capacitor causes a linear increase in voltage across the capacitor. We'll go from there. Can you see why your circuit would convert a square wave into a triangle wave? If you understand a few basic opamp rules you will see the light.

 

[JC2000]

I will first tell you that a constant current through a capacitor causes a linear increase in voltage across the capacitor. We'll go from there.

You are saying that current would cause build up of charge and hence the increase in voltage? If so part of the current through R goes to the amplifier and the signal is amplified while the rest causes a charge build up in the capacitor. However here a have the following question :

If the output current from the amplifier is also splitting into the capacitor and the output then there is charge build up on both sides of the capacitor which doesn't make sense... (assuming I haven't gone wrong upto this point...)


Regarding the square wave to triangle wave conversion :

I broke one cycle of the square waveform into functions (essentially the horizontal lines corresponding to 'constant peaks' on either side).

However integrating these two horizontal lines (say$y = x$ and $y = -x$) gives me two functions ($y = (x^2)/2$ and $y = -(x^2)/2$) which are vertical parabolas ('facing' opposite directions)...I realize I have not substituted the limits of the integral however I don't see how that helps me arrive at the triangular waveform...

 

[Averagesupernova]

You are saying that current would cause build up of charge and hence the increase in voltage? If so part of the current through R goes to the amplifier and the signal is amplified while the rest causes a charge build up in the capacitor. However here a have the following question :

If the output current from the amplifier is also splitting into the capacitor and the output then there is charge build up on both sides of the capacitor which doesn't make sense...

Two rules in linear opamp operation (within the design limits of the device):
1) No current enters or leaves either opamp input.
2) Opamp inputs track each other. What voltage appears on one will appear on the other.
-
Now, rethink it.

 

[JC2000]

Two rules in linear opamp operation (within the design limits of the device):
1) No current enters or leaves either opamp input.
2) Opamp inputs track each other. What voltage appears on one will appear on the other.
-
Now, rethink it.

Since the capacitor plate connected to the output terminal is at the same potential as the output terminal, it must thus develop the same potential (much larger than the input voltage). This seems to create a sort of 'negative feedback cycle'? My thinking is that a positive voltage input produces a large positive voltage at the output as well as developing a large positive potential on the capacitor play connected to the output. This should mean a negative potential is formed on the capacitor plate connected to the input terminal. Assuming I am correct so far, how would this negative potential affect the positive voltage signal being input?

Regarding the virtual ground issue, I am guessing the non-inverting terminal develops a positive voltage which is the same as the voltage of the inverting terminal? (the other case of both being at ground potential?!)

 

[Averagesupernova]

Since the capacitor plate connected to the output terminal is at the same potential as the output terminal, it must thus develop the same potential (much larger than the input voltage). This seems to create a sort of 'negative feedback cycle'? My thinking is that a positive voltage input produces a large positive voltage at the output as well as developing a large positive potential on the capacitor play connected to the output. This should mean a negative potential is formed on the capacitor plate connected to the input terminal. Assuming I am correct so far, how would this negative potential affect the positive voltage signal being input?

Regarding the virtual ground issue, I am guessing the non-inverting terminal develops a positive voltage which is the same as the voltage of the inverting terminal? (the other case of both being at ground potential?!)

The non inverting terminal cannot develop a voltage when it is tied directly to ground.
-
In your circuit, a positive voltage on the left side of the resistor will cause an increasing negative voltage on the output in order to satisfy opamp rule #2.

 

[JC2000]

The non inverting terminal cannot develop a voltage when it is tied directly to ground.
-
In your circuit, a positive voltage on the left side of the resistor will cause an increasing negative voltage on the output in order to satisfy opamp rule #2.

So if the non inverting terminal was not grounded it would have developed the same voltage?

Also, a positive voltage on the input terminal (inverting terminal) causes a negative voltage on the output which should mean a negative potential on the capacitor plate connected to the output terminal? This would mean a positive potential on the capacitor plate connected to the inverting input terminal ? Which suggests a 'positive feedback'? This seems to result in some sort of perpetually increasing potential(?) which seems to contradict energy conservation (?).

With regard to the square wave form :

Considering the constant positive input, shouldn't there be a much larger (in magnitude) but negative constant output instead of a ramp?

 

[Averagesupernova]

So if the non inverting terminal was not grounded it would have developed the same voltage?

If you mean the noninverting terminal was left floating that is not an acceptable design.

Also, a positive voltage on the input terminal (inverting terminal) causes a negative voltage on the output which should mean a negative potential on the capacitor plate connected to the output terminal? This would mean a positive potential on the capacitor plate connected to the inverting input terminal ? Which suggests a 'positive feedback'? This seems to result in some sort of perpetually increasing potential(?) which seems to contradict energy conservation (?).

No. The left capacitor plate will try to follow the right plate. A capacitor opposes a change in voltage across it.

With regard to the square wave form :

Considering the constant positive input, shouldn't there be a much larger (in magnitude) but negative constant output instead of a ramp?

The ramping voltage on the output will continue as long as the voltage on the input remains constant.

 

[Averagesupernova]

I used to work on test equipment that included NTSC video test pattern generators. One of the test patterns was called a staircase. So, your thread caught my eye.

 

[Joshy]

If you're curious about the currents, then why not use KCL at the node between the two elements? Keep in mind what averagesupernova (what an average name I love it) said in the earlier post #4 about the current going into the op-amp and the voltages at the two terminals.

Like this

Solve for $i_1$ and $i_2$ (Ohm's law). You'll be able to solve for your transfer function, which you've already got... you'll also know exactly what's going on with the current (I think you're more curious about $i_2$, right?)

 

[Averagesupernova]

Well I thought about making my username Stupidsmartguy but I thought that might be offensive.
-
Would like to hear back from the OP. I think with a bit of guidance @JC2000 will have it figured out. The light sure turned on in my head when I accepted the two simple rules. It is counter intuitive at first but those two rules allow some serious shortcuts in designing with opamps.

 

[JC2000]

(forgot the dt!)

I think I understand how the integrator works theoretically (as in how the equation is arrived at).

Using the two rules for OpAmps,
a. I think that V+ and V- would be at ground potential. (But how does the amplifier amplify a null input?!)
b. Input signal $V_i$ drops across R to $V-$ which is 0?!
c. The amplifier output is the inverted integral of the input signal (according to the equation).
d. Perplexed about about how this negative potential interacts with the capacitor and how the feedback interacts with the input at the inverting terminal.
e. According to the rules, no current flows through the circuit.


f. So if a square waveform is the input signal, the output would be the inverse of the integral of the square waveform. But this seems to give a constant output signal...

Also, really grateful for your patience!

 

[Baluncore]

Coming at the question from the other direction.

It is impossible to get an instant voltage step from a simple op-amp integrator because the capacitor current would need to be infinite for an infinitesimal time. Likewise it is not possible for an integrator to generate a true rectangular staircase.

Differentiation is the inverse function of integration. To generate a staircase you may need to differentiate an input signal with a high-pass filter, then process that signal, before you integrate using a low-pass filter.

Start with a steep edge digital clock, differentiate the clock signal with a series capacitor, then use a couple of diodes to steer the current spike (= charge dump) into the integrator. Every digital cycle will generate a step in the output. The rise time of the individual steps in the staircase will be slightly longer than the transition time of the input clock.

There are ways of making steeper steps using other techniques, but the rise time of an integrator step will always be a finite ramp.

A digital to analogue converter without an integrator can take fast steps if there is no low-pass filter on the output.
Analogue switches can be used with an integrator to make a triangle wave, that then appears to be a saw-tooth ramp with an extremely steep edge.

 

[Joshy]

It's not a constant output.

You're setting fixed values to your boundary conditions on the integral, and so that very last graph is incorrect because you're plotting for all $t$ when what you've solved for is just for the integral at one point where $t=0.5$ [Another quick note that I would revisit the integral of 0 (it's not $t$)]

You should set your integral to something like this (notice a subtle change in notation using $t'$ by replacing $0.5$ with $t'$).

$$\int_0^{t'} 5\, dt + \int_{t'}^1 0\, dt$$

I would expect behaviour like this (just talking about the integral alone and ignoring the negative from your op-amp equation).

I added the What is usually seen... maybe I'm wrong-- just what I've seen in my textbooks and assumed that it was more common.

Look away from the hand calculations and formulas for a moment to recall what is the output of an integral... it's the area under the curve.

We recognize the integral under a curve is just the area of the square wave so as you move along the highs (the first one ends at $t'$) you'll see that adding small slices (was trying to draw) up to your boundary condition increases the out (across the entire square wave the integral will be $A$); when you move along zero you're adding nothing. The amplitude of your square wave has no negative values, and so you're not going to add any negatives (just like the part I drew in I thought was normally seen).

In real life it could eventually become a constant output, but this is normally not intentional... the op-amps have a supply (rail) and so when the amplitude of the output gets near the rail (usually a few mV below will do the trick) it saturates and won't go any higher- for example it wouldn't make any sense to expect a 5V output when the op-amp is only supplied 3V.

 

[Nik_2213]

Been a while but, to get a first approximation of a staircase, I fed a free-running flip-flop's 'audio' output to a simple 741 integrator. The astable's edges were 'faster' than the 741 slew rate, results sufficed...

( IIRC, 'Art of Electronics' offered several tweaks to bootstrap input impedance, avoid diode losses etc etc... )

Situation is sort of comparable to a 'trad' PSU with half-wave rectifier feeding 50~60 Hz to a big smoothing capacitor: The closer you look, the more complexity and trade-offs ensue. Going to a full-wave bridge rectifier is but the start...

 

[Merlin3189]

Regarding the square wave to triangle wave conversion :

I broke one cycle of the square waveform into functions (essentially the horizontal lines OK corresponding to 'constant peaks' ?? on either side).

However integrating these two horizontal lines (say$y = x$ and $y = -x$) Or preferably, don't say that! gives me two functions ($y = (x^2)/2$ and $y = -(x^2)/2$) which are vertical parabolas...

This is where you go wrong. The top of the square wave is$y=A$ and the bottom is $y=-A$
When you integrate, you get $y= Ax \text{ and } y= -Ax \,$ which are both straight lines, making your triangle wave.

Now, as for your staircase (I forgot you'd asked this when I drew the piccy)
If you look at the differential of the square wave, you see a series of pulses of alternating polarity.
These pulses are interesting beasts, invented, I believe, by Paul Dirac as the delta function. Ideally they have zero width (!) and indeterminate amplitude, but their integral is 1 ( or A if the basic pulse is multiplied by A)

If they sound a bit impossible, that's because you never actually get square waves that change from -1 to +1 in zero time. A square wave is equally imaginary - this time I think imagined by Oliver Heaviside as an extension of his step function.

So in practice we get an approximate square wave by integrating a series of finite positive and negative pulses. The width of the pulse limits the rise time of the square wave, because, asyou know, integrating a pulse (like the blocks of a square wave) gives you a straight slope. So integrating a series of alternating, very short pulses will give you a trapezium wave - long pulses with sawtooth sides. (Diagram to follow)

Anyhow, that leads to the simple answer to your staircase: integrate a series of pulses (ideally delta pulses) of the same polarity. Each pulse causes a new half cycle of a square wave, but always in the same direction.

That's all on paper. You are limited by the response of your integrator and by the size of the pulses you can generate. But everyone else has flogged that horse to death and it should be fairly easy to get decent results up to anything you can see on your average oscilloscope.

 

[Merlin3189]

A bit rushed, but I hope it shows enough. I had to squash the staircase a bit, as I ran out of screen!

 

[JC2000]

2) Opamp inputs track each other. What voltage appears on one will appear on the other.

Please accept my apologies for coming back to this!
So if one input is grounded and we are providing the other input then as the grounded input can never be a non zero value, the other input will always be zero (because of virtual grounding)?

 

[JC2000]

It's not a constant output.

You're setting fixed values to your boundary conditions on the integral, and so that very last graph is incorrect because you're plotting for all $t$ when what you've solved for is just for the integral at one point where $t=0.5$ [Another quick note that I would revisit the integral of 0 (it's not $t$)]

You should set your integral to something like this (notice a subtle change in notation using $t'$ by replacing $0.5$ with $t'$).

$$\int_0^{t'} 5\, dt + \int_{t'}^1 0\, dt$$

I would expect behaviour like this (just talking about the integral alone and ignoring the negative from your op-amp equation).

View attachment 258308
I added the What is usually seen... maybe I'm wrong-- just what I've seen in my textbooks and assumed that it was more common.

Look away from the hand calculations and formulas for a moment to recall what is the output of an integral... it's the area under the curve.

We recognize the integral under a curve is just the area of the square wave so as you move along the highs (the first one ends at $t'$) you'll see that adding small slices (was trying to draw) up to your boundary condition increases the out (across the entire square wave the integral will be $A$); when you move along zero you're adding nothing. The amplitude of your square wave has no negative values, and so you're not going to add any negatives (just like the part I drew in I thought was normally seen).

In real life it could eventually become a constant output, but this is normally not intentional... the op-amps have a supply (rail) and so when the amplitude of the output gets near the rail (usually a few mV below will do the trick) it saturates and won't go any higher- for example it wouldn't make any sense to expect a 5V output when the op-amp is only supplied 3V.

1. I am really sorry for going AWOL like this.
2. Thank you for the response! I think I understand now...
3. Since the integrator is an inverting integrator the triangular waveform would be out of phase with the square waveform? And the 'rising staircase' waveform would be reflected on the x -axis (head downward) because of the inverting bit?
4. So the integral of a function is a function whose output is the area under the curve for the original function for whatever limits are chosen (?!). Hence the variable in the limit and so when I put in actual values I ended up getting the value for the area whereas I was looking for the function?
5. I think I have understood(?!). Thank you for your time and apologies for coming back to this!

 

[JC2000]

If you're curious about the currents, then why not use KCL at the node between the two elements? Keep in mind what averagesupernova (what an average name I love it) said in the earlier post #4 about the current going into the op-amp and the voltages at the two terminals.

Like this
View attachment 258231

Solve for $i_1$ and $i_2$ (Ohm's law). You'll be able to solve for your transfer function, which you've already got... you'll also know exactly what's going on with the current (I think you're more curious about $i_2$, right?)

Did you assign some directions for $i_1$ and $i_2$ or are they obvious somehow?!
When applying KCL would it be $V_i - V^{-}$ or the reverse?

 

[Joshy]

It doesn't matter which direction you assign them. The math will correct the answer. If you draw them the "wrong" way, then you'll get a negative current (for example if it's -100 mA when you drew the arrow left, then you know it's 100 mA going right, the problem is solved and both are valid answers). What I like to do is draw all the currents in the same direction either all in or all out and the sum of them add up to zero. If you don't draw them all the same direction, then you have to do very careful bookkeeping of the sign.

I would expect for you to find one of my old posts in a different thread, but I draw it out for someone and show them a voltage divider example. Maybe it'll be helpful for you.

My personal preference is to make them all face the same direction ie. all inward or all outward. I don't have to worry about any bookkeeping and I'll let the mathematics dictate the direction.

Something like this:

Here's an example with a classic Voltage Divider. I know it's simple, but the point is to show that the direction didn't matter.

 

[Dullard]

"So if one input is grounded and we are providing the other input then as the grounded input can never be a non zero value, the other input will always be zero (because of virtual grounding)?"

You may be reading too much into that 'rule.' An ideal OP-AMP will drive the output positive when the non-inverting input is more positive than the inverting input (and negative when the opposite is true). the 'virtual ground' behavior is the result of properly selected/arranged external components.

 

[JC2000]

"So if one input is grounded and we are providing the other input then as the grounded input can never be a non zero value, the other input will always be zero (because of virtual grounding)?"

You may be reading too much into that 'rule.' An ideal OP-AMP will drive the output positive when the non-inverting input is more positive than the inverting input (and negative when the opposite is true). the 'virtual ground' behavior is the result of properly selected/arranged external components.

So the rule can only be applied if there is some feedback ? As the Op Amp can only control the output, if there is feedback then it can control the input and thus in effect 'enforce' such a rule?!

 

[Dullard]

Correct.

 

[JC2000]

Correct.

Just needed a clarification.
In the case of an ideal open loop op amp however would the virtual ground concept be applicable (since gain is infinite)?

 

[Baluncore]

Just needed a clarification.

With the non-inverting input at ground potential, a virtual ground only exists if feedback from the op-amp output to the inverting input balances the input voltages.

 

[JC2000]

With the non-inverting input at ground potential, a virtual ground only exists if feedback from the op-amp output to the inverting input balances the input voltages.

Yes but wouldn't virtual ground also exist when it is an ideal op amp in open loop? Since it is ideal the gain is infinity and thus the two inputs must be at same potential so that their difference is zero?

 

[Joshy]

No. Inside of the output of the op-amp it's modeled like a dependent source; it's dependent on the voltage difference between the two inputs. When there is feedback that dependent source causes current to be driven in such a way, that it pulls the voltage to be the same at the input.

 

[Baluncore]

The virtual ground concept simplifies the analysis of some op-amp circuits.
It does that by making possible a local node with a known fixed voltage and a sum-zero current.
It assumes the op-amp has infinite open-loop gain, and it requires a closed negative feedback loop.

 

[Baluncore]

Yes but wouldn't virtual ground also exist when it is an ideal op amp in open loop? Since it is ideal the gain is infinity and thus the two inputs must be at same potential so that their difference is zero?

Ground the (+)input of the op-amp. Then consider two possibilities.

1. Connect the output to the (–)input. You have a voltage follower that is simply buffering ground, which is unnecessary. It is introducing an input-offset voltage, and wasting supply current to do that.

2. Ground the (–)input. The output voltage will be the offset input voltage multiplied by the open-loop gain. The (–)input will be a real ground, not a virtual ground.