joelkato1605
- 19
- 2
- Homework Statement
- You are several meters under water (η = 1.33), swimming in a pool, and look skywards. Light from outside the pool will form a cone. Describe why and compute the
angle of the cone.
- Relevant Equations
- snell's law
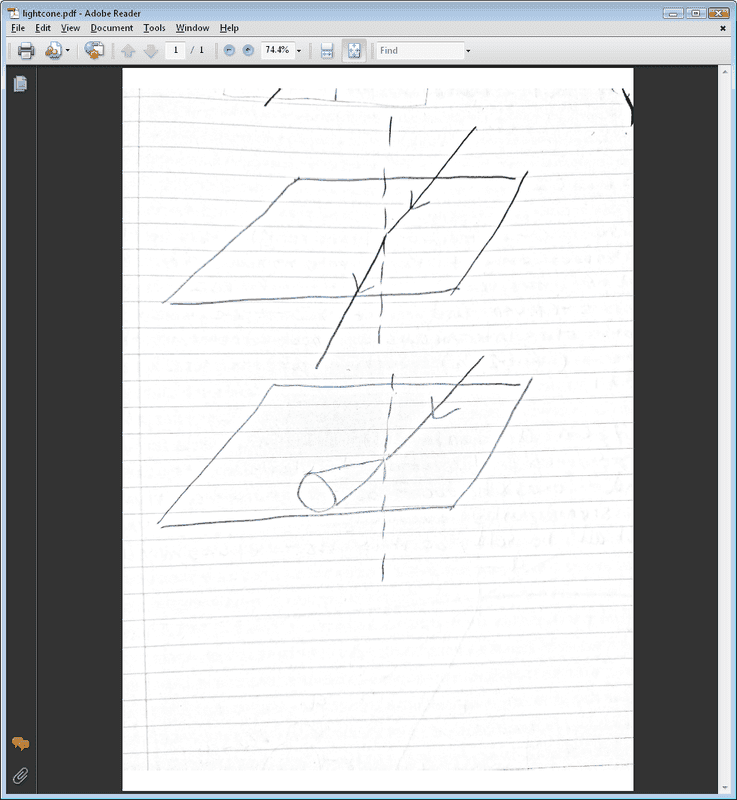
The first sketch is what I assumed would happen, where the light beams bends. And the second is meant to depict the light forming a cone, which I don't understand.
[Mentors provided help re-posting the image that was missing]
[Mentors provided help re-posting the image that was missing]
Attachments
Last edited by a moderator:
 !
! 