Why is Julius Sumner Miller saying Torricelli's law is not correct?

[Yonut]

TL;DR

A video of Julius Sumner Miller from a TV show in the 70's suggests that Torricelli's law is not entirely correct. He says text books have been wrong for centuries. If this is so, why are people still using Torricelli's law?

Hello,

I'm just starting my research on a project I would like to build. But the design on the project has been delayed until I can get a concrete answer to this problem.

I grew up loving the "The Professor" segments on a kids show from the 70's called "The Hilarious House of Frightenstein". It was hosted by Dr. Julius Sumner Miller. In one episode, he talks about Torricelli's law with a three holed can. The holes are placed at 1/4, 1/2 and 3/4 the distance from the top of the can. Julius suggests that the top and bottom holes will cover the same distance from the can when draining. He then suggests that the middle hole will be the strongest and go the furthest from the can. He states the distance from the can, from the middle hole, will be equal the the water height in the can.

He then goes on to say how, the diagram relating to Torricelli's law, is wrong and has been wrong for centuries in textbooks.

So I try to confirm this on the web, but all I come across are diagrams using Torricelli's law. The same one, Julius suggests are incorrect.

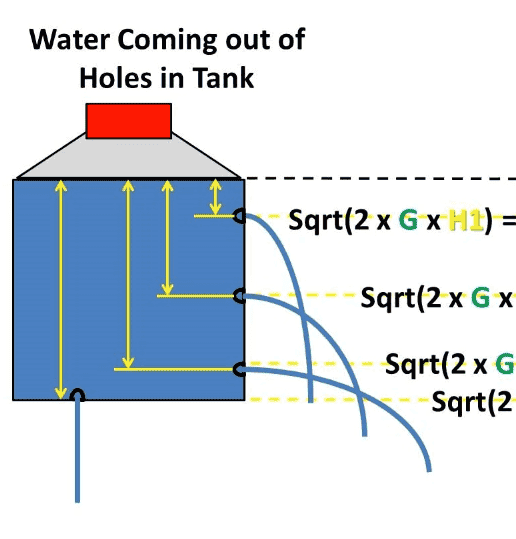
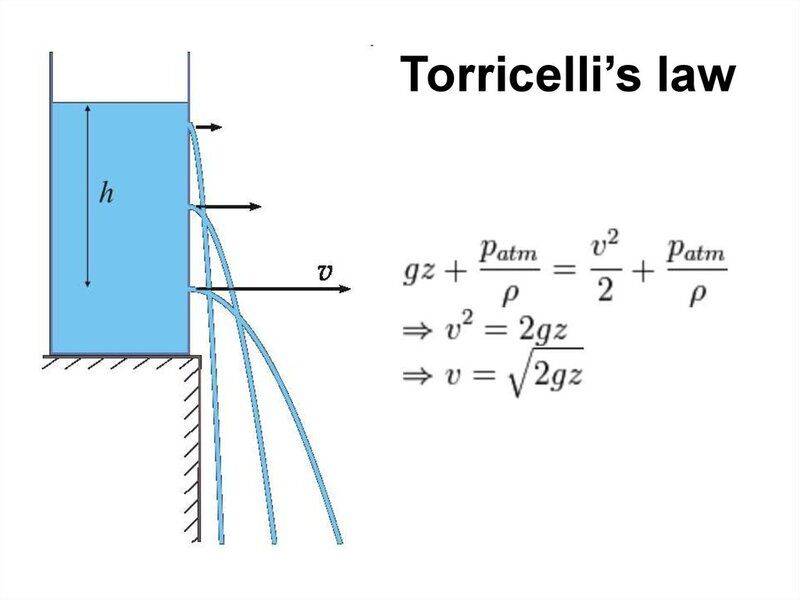
All of the attached diagrams suggest the lowest hole will have the strongest jet (cover the furthest distance).

Here is the link to Julius's solution segment (as this experiment spanned two episodes):
Julius Sumner Miller 20 HHOF - The Case of the Three Holed Can Cont.

I understand you can't trust most of the people that are allowed to permeate the television waves. But Julius, I feel being so popular, would have been called out for such a wrong statement, if it were indeed wrong. So please can someone shed some light on this. I really just want to know if the middle hole indeed has the strongest jet, or if it is the bottom hole.

Ty.

 

[kuruman]

$\dots$ suggest the lowest hole will have the strongest jet (cover the furthest distance).

Here is your misconception. Even though the lower hole has the strongest jet, the water from it does not necessarily go farther because it stays in the air for a shorter time. Do the math and you will see that the Professor is correct.

Let
L = Height of the column from the ground.
h = The distance from the ground to a given hole.

Then the speed of the water coming out of a hole is $v=\sqrt{2g(L-h)}.$
The time of flight is $t_f=\sqrt{\dfrac{2h}{g}}$.
The range is $R=vt_f=2\sqrt{h(L-h)}$.

How does the range at $h=\frac{3}{4}L$ (highest jet) compare with the range at $h=\frac{1}{4}L$ (lowest jet)?
What about the range of the middle jet at $h=\frac{1}{2}L$?

 

[Yonut]

Tyvm.

 

[kuruman]

Yvw.

 

[PeroK]

View attachment 291348All of the attached diagrams suggest the lowest hole will have the strongest jet (cover the furthest distance).

This diagram from the Wikipedia page clearly shows the lowest jet being the strongest, yet the middle jet having a greater range, as measured at the base of the container. There's nothing wrong there.

I wasn't very impressed by Dr JSM as he seemed more intent on the point that everyone else was wrong without explaining why he was right - and not taking the time to explain why they were wrong - by sloppily equating the strength of the jet to the range at the base of the container.

If he had explained it properly, you wouldn't have had to post here to get a more sober and less dramatic exposition from @kuruman

The other two diagrams are inaccurate, as they make the sloppy mistake that Dr JSM avoided explaining.

 

[kuruman]

Here is a plot showing the ratio of the range $R$ to the column height versus the ratio of the hole height to the column height. Note that the range is double-valued for heights other than the middle of the column where there is a maximum. The shape is half an ellipse with equation $r^2+4\left(h-\frac{1}{2}\right)^2=1.$