Why Is the Boltzmann Factor Exponential?

[Glenn G]

Hi community, trying to get my head around the Boltzmann factor...

e^(-E/kT)

It states in a book I'm reading that this is linked to the probability of a particle moving from its current energy state to an energy state E above it? So if you were looking at an energy jump of 4kT that the probability of a particle making this jump is :

e^(-4kT /kT) = e^(-4) = 0.0183 so like saying if there were 10,000 particles at temp. T that around 183 would make the transition. Is this the correct interpretation? What I'm not sure about is is there any time scale associated with this?

OK so I sort of get the concept that 183 out of 10,000 particles giving you 0.0183 represents a probability but I don't get where the exponential relationship comes from. Where did Boltzmann get this exponential relationship from and convinced himself that this modeled proabilities on a microscopic scale.

I read part of a book by Teller (old one) and it was saying that the e^(-E/kT) was like the probability of finding a particle? (don't really get this) and that say two particles (E1, E2 initially) collide the probability of finding the 2 particles afterwards has to be the same as before the collision and that from the conservation of energy, this has to be conserved also and that the exponential relationship is the only one where energy conservation holds in a collision because energies add,
e^(- (E1' + E2') /kT) (E1' E2' are the energies after the collision)

whereas probabilities multiply
e^(-E1'/kT) * e^(-E2'/kT)

Not really firm on this interpretation, would appreciate any input.

There is an analysis on wiki I've seen that goes into a derivation of how the density of the atmosphere changes with height and it goes into deriving an exponential relationship (see part below)

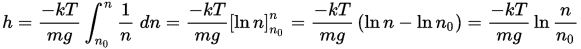
I can follow this route to showing why the density of gas drops exponetially with height but I still don't see how this necessarily assumes that the exponential relations e^(-E/kT) is applicable to so many other scenarios.
Would welcome any input/help.
Glenn.

 

[mfb]

It is not the probability of transitions, it is the relative probability of finding something in this state at any given point in time.

If you only have the ground state and a state 4 kT higher, you'll find a fraction of 1/(1+0.0183) in the ground state and a fraction of 0.0183/(1+0.0183) in the higher state. With more than two states, extend the formulas accordingly: the numerator is the Boltzmann factor of the state, the denominator is the sum of the Boltzmann factors of all states.Deriving that is not easy. You want to find an energy distribution that is stable over time.

For gas atoms, you can use the collision process: For a given distribution, the collisions should not change the distribution over time. The exponential distribution is the only one that fits.

In statistical physics, you can generalize this approach to all systems with different energy levels, but that is beyond the scope of high school physics.