Why is the refractive index for red lower than for blue?

[spareine]

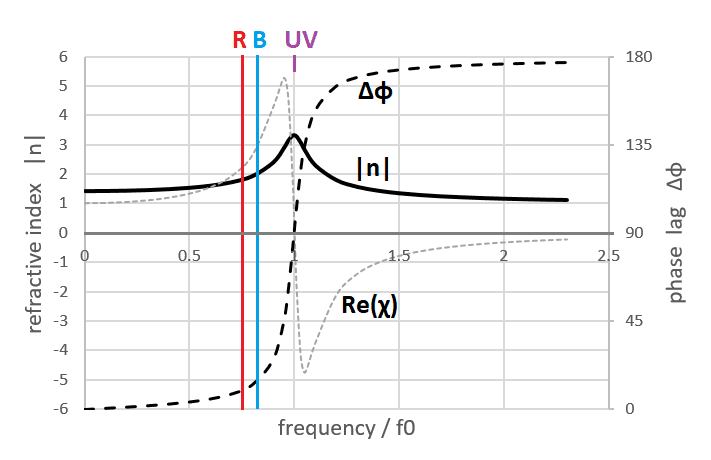
By observing that red is the outermost color of the rainbow it is possible to conclude the refractive index of water, n, is lower for red than for blue. However, why is n lower for red? This seems to be answered by the Drude dispersion model, with a resonance in the ultraviolet region, but I don't get it because by definition n is related to the speed of light, v, whereas the Drude model discusses the electric susceptibility, χ, as a function of the frequency f, without mentioning the speed of light. In the Drude model n is introduced indirectly by the equation n² = 1+χ. Should the phase lag of the Drude model, Δφ, be used to explain the variation of v? (Like: v(f) is monotonic increasing because Δφ(f) is monotonic increasing, at the left side of the graph)

 

[Dale]

by definition n is related to the speed of light, v, whereas the Drude model discusses the electric susceptibility, χ, as a function of the frequency f, without mentioning the speed of light

Isn’t the speed of light related to the susceptibility?

 

[spareine]

Isn’t the speed of light related to the susceptibility?

Apparently my intention is unclear, so let me rephrase. Yes, n² = 1+χ, but when possible I am interested in a visual image of the mechanics of how the propagating wave is delayed, instead of equations that do not contain the propagating wave. Somehow the Drude model seems to facilitate such a visual image, but the only time parameter provided by the model seems to be the phase delay. I am simply unsure about how to use the phase delay.

 

[Lord Jestocost]

When regarding the propagation of light in a medium with attenuation, one has to exchange the simple refractive index by a complex refractive index that is directly related to the complex dielectric function. See, for example:

https://www.tf.uni-kiel.de/matwis/amat/elmat_en/kap_3/backbone/r3_7_1.html
https://www.tf.uni-kiel.de/matwis/amat/elmat_en/kap_3/backbone/r3_7_2.html
https://www.tf.uni-kiel.de/matwis/amat/elmat_en/kap_3/backbone/r3_7_3.html

 

[spareine]

Ah, I found an old post on physics forum, "Microscopic reason why refractive index typically increases with frequency?", that uses the Drude model and its phase delay to explain that the refractive index increases with frequency. Still not entirely clear to me, unfortunately (because in that post, 180° should be 90°, I think, and because it says the amplitude has an effect on the speed as well)

When regarding the propagation of light in a medium with attenuation, one has to exchange the simple refractive index by a complex refractive index that is directly related to the complex dielectric function. See, for example: …

Thanks! The Drude model uses a complex refractive index as well (n² = 1+χ, where χ is complex)

 

[Cthugha]

Ah, I found an old post on physics forum, "Microscopic reason why refractive index typically increases with frequency?", that uses the Drude model and its phase delay to explain that the refractive index increases with frequency. Still not entirely clear to me, unfortunately (because in that post, 180° should be 90°, I think, and because it says the amplitude has an effect on the speed as well)

No, the phase delay is only 90° exactly at resonance. Above resonance it quickly approaches 180° as stated correctly in that old post. Actually, the physics behind the behavior at resonance is not different from a driven antenna or any other periodically driven harmonic oscillator. If you drive it below resonance, the oscillating charge follows the external force exactly and almost instantaneously. At resonance, there is a 90° phase shift, which yields the typical resonance behavior and above resonance you get the 180° phase shift, which is the typical "force that points in the opposite direction of the displacement" scenario.

 

[spareine]

Thanks, in the way you rephrased "slightly above the resonance frequency, the oscillator is 180 degree out of phase", it corresponds better to the Δφ-f graph that I made in post #1 on basis of the exact equations of the Drude model.

I still do not understand the remainder of the old post:

In the case of light, the phase velocity of light will be higher than in vacuum as the emitted wave appears to have "jumped forward" in comparison with the driving light wave. However, the amplitude decreases when the frequency increases so that the phase velocity of the light will decrease, too.

When using a continuous wave, I don't understand why the phase velocity would be higher than in vacuum.

 

[Cthugha]

Note that we are talking about really high frequencies here. The region, where the refractive index is below one is usually in the x-ray region at frequencies higher than all bound resonances in the system. Here, the physics is somewhat simple. The incoming light wave will cause the electrons the perform oscillatory motion, which will in turn result in the electrons emitting light again. The light wave behind the material will be the superposition of the initial light field $E_0$ and the re-emitted light field by the electrons $E_s$. As you can see from the phase lag of 180°, this means that in the high frequency region, you will get something like $E_s= - E_0*k$, where k is some complex value that includes plenty of effects: wavelength, density of electrons and so on. If you do the math, you will find that light field behind the material is roughly speaking something like $E= E_0 (1-k)$, which directly translates to a refractive index slightly below one.

If this is still puzzling, have a look at the Feynman lectures, chapter 31 (http://www.feynmanlectures.caltech.edu/I_31.html).