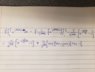- #1
Why Multiply by Exponential Terms in Fourier Series Calculations?
- Context: Engineering
- Thread starter lottotlyl
- Start date
Click For Summary
Discussion Overview
The discussion revolves around the use of exponential terms in Fourier series calculations, particularly focusing on the manipulation of terms involving sine functions and complex identities. Participants explore the application of calculus and algebra in this context.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Homework-related
Main Points Raised
- One participant mentions difficulty in applying a complex identity for the sine function, indicating a potential challenge in the calculations.
- Another participant references the fundamental theorem of calculus and suggests that both calculus and complex analysis are necessary for the problem at hand.
- A participant expresses uncertainty about the subsequent steps after obtaining an initial result.
- It is proposed that multiplying by an exponential term, specifically $$e^{\frac{-j\pi k}{3}}$$, could be beneficial, suggesting a strategy to simplify or manipulate the expression further.
Areas of Agreement / Disagreement
Participants do not appear to reach a consensus, as there are indications of uncertainty and differing approaches to the problem.
Contextual Notes
Some assumptions regarding the application of complex identities and the steps involved in the Fourier series calculations remain unclear, and the discussion does not resolve these uncertainties.
Who May Find This Useful
Individuals interested in Fourier series, complex analysis, and mathematical techniques in physics or engineering may find this discussion relevant.
- #2
Gaussian97
Homework Helper
- 683
- 412
Applying the fundamental theorem of calculus which says that
$$\int_a^b f(t)dt=F(t)\Big|_a^b=F(b)-F(a)$$ where ##F(t)## is a function satisfying $$\frac{dF(t)}{dt}=f(t).$$
Then you also need to use elemental algebra and complex analysis.
$$\int_a^b f(t)dt=F(t)\Big|_a^b=F(b)-F(a)$$ where ##F(t)## is a function satisfying $$\frac{dF(t)}{dt}=f(t).$$
Then you also need to use elemental algebra and complex analysis.
- #3
- #4
Gaussian97
Homework Helper
- 683
- 412
Well, notice that in the final answer you have the term $$e^{\frac{-j\pi k}{3}}$$ so it would be a good idea to multiply by $$1=e^{\frac{-j\pi k}{3}}e^{\frac{j\pi k}{3}}.$$
Similar threads
Engineering
Fourier transform of a shifted sine wave
- · Replies 3 ·
- · Replies 3 ·
- · Replies 3 ·
- · Replies 26 ·
- · Replies 4 ·
- · Replies 3 ·
- · Replies 1 ·
- · Replies 6 ·