Why the at term on the exponential turned positive

[Firepanda]

Firstly, I don't get why the at term on the exponential turned positive (red arrow).. can someone explain that please?

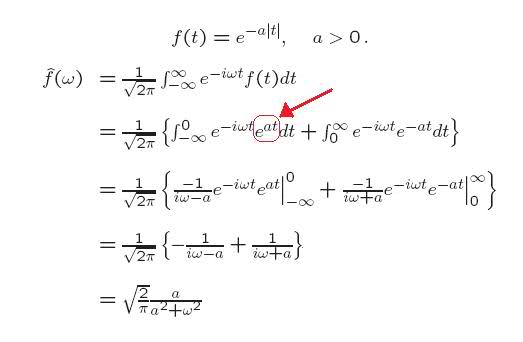
And how do I start on this? How do I split it up such that I can do it for t>0 and t=<0?

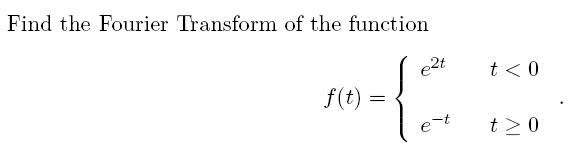
Do I just integrate e^2t between -inf and 0 and integrate e^-t between 0 and inf?


Thanks!

 

[dx]

What is |t| when t is negative?

 

[Firepanda]

What is |t| when t is negative?

positive, ah I see now, thanks

still stuck on 2nd though

edit: actually why would that change the sign of the a?

 

[dx]

Just split the integral into two parts, one on (-∞,0) and the other on (0,∞).

 

[Cyosis]

edit: actually why would that change the sign of the a?

You should really draw f(t)=e^{|t|}. And then give a function that represents f(t) in the first quadrant and f(t) in the second quadrant.

 

[dx]

|t| = -t by definition when t is negative.