Why use arbitrary voltage source in Dependent Thevenin's

[yosimba2000]

Normally, I would just assume that for a circuit with just a dependent source, I can treat it the same as as one with an independent source.

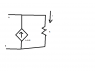
Using Picture 1
Assume that I want to find the Thevenin wrt nodes A and B.
I want to find Rth, so I zero out all sources, which makes I = 0A. The only resistance left is from resistor R.
I call R my Rth.

But this is wrong!

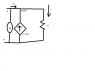
Using Picture 2
Apparently, I have to attach an arbitrary voltage source with voltage Vx, which drives an arbitrary current Ix.
Rth = Vx/Ix
So doing KCL on Node C, I get Ix + I = i (1)
I = 0.5i from the picture and plugging into (1)
Ix + 0.5i = i.
Ix = 0.5i (2)
Node C is at potential Vx.
i = Vx/R from the picture, then plugging into (2)
Ix = 0.5(Vx/R)
Rth = Vx/Ix
Rth = Vx / (0.5Vx/R)
Rth = 2R

As you can see, the Rth obtained from both methods is different (the second method is correct), but why, for circuits with only dependent sources, must we apply an arbitrary voltage source to find Rth? What's wrong with the first method?

If it's not clear, here is a video doing the same thing, but with arbitrary current source.

He states that this is the ONLY way to solve for Thevenin Equivalent when there are no independent sources. Why?

 

[cnh1995]

but why, for circuits with only dependent sources, must we apply an arbitrary voltage source to find Rth? What's wrong with the first method?

According to Thevenin's theorem, Rth (Thevenin's resistance) is the resistance of the circuit "seen" by an independent voltage source(Vth) connected between the concerned points (here, a and b). If there is no independent source, everything becomes 0 and the circuit becomes meaningless. Dependent sources depend upon the quantities(voltage or current) which are generated by independent sources. So, Thevenin's resistance and Thevenin's voltage matter only when there is at least one independent source in the circuit.

Using Picture 1
Assume that I want to find the Thevenin wrt nodes A and B.
I want to find Rth, so I zero out all sources, which makes I = 0A. The only resistance left is from resistor R.

Since there is no current, why don't you call it an open circuit? Instead of saying only resistance is R, can you take it out and say it is an open circuit with infinite resistance? Or, since there is no current, there is 0 voltage across the resistor R. But does that make it a short circuit? No. Because there is no driving voltage, therefore no current. If there is an independent voltage source (or current source) present, then only it will "see" the resistance offered to it. So, there should be an independent source in the circuit. If there isn't, one is assumed and then Rth and Vth are calculated as "seen" by that source.