Understanding dependent sources in electric circuits

[zenterix]

TL;DR Summary

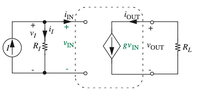
In the shown depictions of a dependent source there is an input side and an output side. How exactly are they connected?

The amount of voltage provided by an independent voltage source and the amount of current provided by an independent current source do not depend on the circuit they are in.

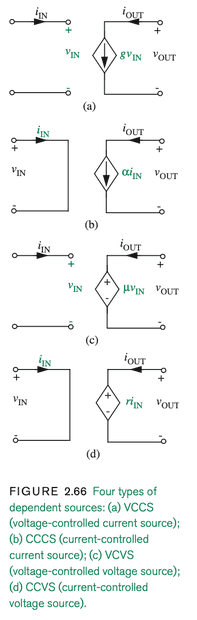
There are other types of sources, however, that do depend on the circuit they are in. That is, such dependent sources depend on (ie, are controlled by) other parameters in the circuit.

Here are depictions of four types of dependent sources

To summarize my question: how is the left side connected to the right side in practice?

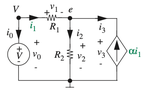
For example, consider the following circuit containing a current controlled current source (case b above)

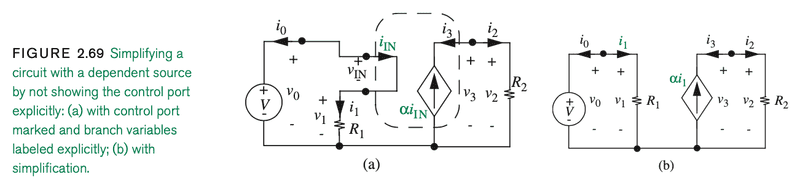
How exactly is it that the depicted input port affects the dependent current source?

I see that there is a connection in the center bottom. Is the connection between the input side and output side as simple as this or is the depiction somehow simplified?

It seems there must be some other connection. As far as I can tell, basic circuit analysis would predict no current in the bottom connection part.

 

[DaveE]

These are idealized circuit models. There is no "why, or how", it is defined to be that way; by magic, I suppose. You can not build this circuit element in the real world, but they can be useful things to build simple models of real world processes... sometimes.

 

[LvW]

The question cannot be answered in general, because the "connection" between input and output is physically different for each active element working as a "dependent source".
But if you know the working principle of the electron tube or the transistors (FET or BJT), then the answer is automatically given.

 

[alan123hk]

It seems there must be some other connection. As far as I can tell, basic circuit analysis would predict no current in the bottom connection part

The basic input-output relationship of the two-port network is defined by the equation. Whether there is a bottom connection depends on your application and decision. If connected together the potential is the same, if not connected the potential difference is undefined
For example, there is no connection between the input and output of an isolation transformer through which actual current can pass.

 

[zenterix]

The question cannot be answered in general, because the "connection" between input and output is physically different for each active element working as a "dependent source".
But if you know the working principle of the electron tube or the transistors (FET or BJT), then the answer is automatically given.

How about if we limit the scope to a specific example?

Below is an example of a circuit containing a CCCS. I still can't really see/understand the mechanism by which the dependent current source depends on a specific current $i_1$ below.

Consider the following reasoning that appears in the book I am reading.

We have the following general depiction of a circuit containing a dependent current source

Now suppose that the circuit on the left has the node voltages as shown below

Then we can express the element law for the dependent source as a function of the node voltages:

$$I=f(i)=f\left (\frac{e_a-e_b}{R}\right )$$

And then the book gives a concrete example:

This circuit has one dependent source, namely a CCCS (current controlled current source).

To analyze this circuit using the node method, we first replace its CCCS with an independent current source carrying a known current, say $I$, and analyze the resulting circuit.

The circuit becomes

We can easily solve the above circuit with the node method, and the solution for $i_1$ is

$$i_1=-\frac{R_2}{R_1+R_2}I+\frac{1}{R_1+R_2}V$$

Of particular interest is the value of $i_1$ because $i_1$ controls the CCCS. Using the result for $i_1$ we next write

$$I=\alpha i_1=\left ( -\frac{R_2}{R_1+R_2}I+\frac{1}{R_1+R_2}V \right )\tag{3.49}$$

and we solve for $I$

$$I=\frac{\alpha}{R_1+(1+\alpha)R_2}V\tag{3.50}$$

The actual value of the CCCS is now known

Finally we back-substitute Equation 3.50, namely the actual value of $I$, into the equations that formed the solution of the circuit in Figure 3.10, thus completing the analysis of the circuit in Figure 3.26.

We get all the solutions in terms of just $V$ and no longer $I$.

For example,

$$i_1=\frac{1}{R_1+(1+\alpha)R_2}V$$

 

[berkeman]

Perhaps look into how Current Mirrors work:

https://www.analogictips.com/how-do-you-use-a-current-mirror-faq/

 

[Dullard]

It has been accurately pointed out that dependent sources are 'ideal' devices. It is worth noting that completely 'independent' devices are also 'ideal.' Coping with the difference between ideal and actual is one definition of Engineering.

 

[alan123hk]

Perhaps look into how Current Mirrors work

Should this be a current-controlled current source, a current-controlled voltage, a voltage-controlled current source or a voltage-controlled voltage source?
If it is CCCS, it corresponds I_OUT /I _REF
If it is CCVS, it corresponds V_OUT / I_REF
If it is VCCS it corresponds I_OUT /V _CC
If it is VCVS, it corresponds V_OUT / V _CC
It seems that this circuit contains four possibilities

 

[berkeman]

Should this be a current-controlled current source, a current-controlled voltage, a voltage-controlled current source or a voltage-controlled voltage source?
If it is CCCS, it corresponds I_OUT /I _REF
If it is CCVS, it corresponds V_OUT / I_REF
If it is VCCS it corresponds I_OUT /V _CC
If it is VCVS, it corresponds V_OUT / V _CC
It seems that this circuit contains four possibilities

Vcc sets Iref, so in a sense it is a VCCS.

 

[berkeman]

Here's another way to use an opamp and transistor to make a VCCS:

https://circuitdigest.com/electronic-circuits/voltage-controlled-current-source-circuit-using-op-amp

 

[alan123hk]

I totally agree it's a VCCS.

1. The circuit diagram has marked the input as a voltage source.
2. The output of the circuit is a current source that changes with the input voltage, so the output current will not be affected by the battery voltage.
3. It is impossible to claim that this is a VCVS because the constant voltage of the battery is not affected by the input voltage or output current.

Sorry, I haven't looked at this circuit diagram in detail before.

 

[DaveE]

Also, the Howland Current Source is a standard op-amp solution.

 

[Tom.G]

Here is a perhaps easier equivalent to a CCCS; that is a Current Controlled Current Source.

Consider an LED light emitter. The light output is directly proportional to the current flowing thru it.

Next to the LED is a photovoltaic cell; that is a photocell that can supply a current proportional the intensity of light falling on it.

The more current thru the LED, the brighter it is, the more light that hits the photocell, the more current the photocell can supply.

There is no need for an electrical connection between the two.

In fact, that is how fiber-optic communication works; an LED or a LASER diode emits light that travels thru the fiber, and a photodetector at the far end detects the light.

A simpler version of the fiber-optic communication is an opto-isolator. That is a device that puts the LED and the photocell all in one package. It is packaged like an integrated circuit (IC) and uses light to isolate two parts of a circuit that are at different voltages.

Hope this Helps!
Tom

 

[alan123hk]

Also, the Howland Current Source is a standard op-amp solution.

This Howland Current Source should be very useful in practice, its simply $~~i_o=\frac {V_i} {R_1 }~$ and the direction of $i_o$ can be changed depending on the polarity of $~V_i$

 

[berkeman]

Also, the Howland Current Source is a standard op-amp solution.

That's weird. I need to think more about that circuit...

 

[zenterix]

Here is a perhaps easier equivalent to a CCCS; that is a Current Controlled Current Source.

Consider an LED light emitter. The light output is directly proportional to the current flowing thru it.

Next to the LED is a photovoltaic cell; that is a photocell that can supply a current proportional the intensity of light falling on it.

The more current thru the LED, the brighter it is, the more light that hits the photocell, the more current the photocell can supply.

There is no need for an electrical connection between the two.

In fact, that is how fiber-optic communication works; an LED or a LASER diode emits light that travels thru the fiber, and a photodetector at the far end detects the light.

A simpler version of the fiber-optic communication is an opto-isolator. That is a device that puts the LED and the photocell all in one package. It is packaged like an integrated circuit (IC) and uses light to isolate two parts of a circuit that are at different voltages.

Hope this Helps!
Tom

How does the photovoltaic cell supply current to the LED without an electrical connection? I thought the photovoltaic cell produced current that flowed through the LED (by way of an electrical wire).

 

[Tom.G]

How does the photovoltaic cell supply current to the LED without an electrical connection?

It doesn't.
The LED is only the input side, the side where the signal comes in and powers the LED.
The Photovoltaic cell is the output, it does not need, and often does not have, any electrical connection to the LED.

Cheers,
Tom

 

[alan123hk]

Looking at the equivalent circuit of a solar cell, the energy it outputs basically comes from a current source ($I_L$) that is proportional to the intensity of light received
https://en.wikipedia.org/wiki/Theory_of_solar_cells

 

[DaveE]

A comment about sources in linear networks:

We know that the Thevenin-Norton source transformation theorems say that any voltage source branch can be expressed as a current source, and vice-versa. Like this:

Where In = Vt/Rt or Vt = In⋅Rn and Rt = Rn.

So, in practice, what really is the difference between a current source and a voltage source? It's simply the value of $Rt=Rn$ compared to the other impedances in the circuit. Current sources are very high impedance so that $\frac{\partial i}{\partial v} \approx 0$; the output current doesn't change much if the output voltage changes. Voltage sources are very low impedance so that $\frac{\partial v}{\partial i} \approx 0$; the output voltage doesn't change much if the output current changes. Note that these derivatives are the definition of the source impedance $\frac{\partial v}{\partial i} =Rt=Rn$.

IRL, sources live on a continuum with most somewhere in between.

Also note that a perfect voltage source with $Rt=0$ can't be transformed into it's Norton equivalent and vice-versa. However, as soon as you connect it to a network, it can be converted using the driving point impedance of the network.

 

[alan123hk]

Finally we back-substitute Equation 3.50, namely the actual value of I, into the equations that formed the solution of the circuit in Figure 3.10, thus completing the analysis of the circuit in Figure 3.26.

We get all the solutions in terms of just V and no longer I.

You define CCCS in the circuit and get equation $~~ i_1=\frac{1}{R_1+(1+\alpha)R_2}V$.
So do you feel like you now have a good understanding of the dependent sources in general circuits?