Why Use Sin 53° Instead of Sin 37° for Torque Calculation?

[PeachBanana]

Homework Statement

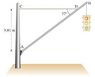
A traffic light hangs from a pole as shown in the figure . The uniform aluminum pole AB is 7.50 m long and has a mass of 12.0 kg. The mass of the traffic light is 21.5 kg.

Homework Equations

clockwise torques = counterclockwise torques

The Attempt at a Solution

This may seem silly but my professor said to use the sin of 53° but one of the tutors told me to use the sin of 37 ° (which ended up being incorrect) because of the parallel line theorem. Could someone explain to me why the tutor was mistaken?

(12.0 kg)(3.75m)(9.8 m/s^2)(sin 53°) + (21.5 kg)(9.8 m/s^2)(7.50 m)(sin 53°) = F * 3.80 m

 

[PhanthomJay]

The tutor may have just erred in the geometric or trigonometric relationships. The moment, M, of a force, F, about a point, is the cross product of the position vector, r, times the force , that is, M = r X F = (r)(F)(sin theta), where theta is the angle in between the force and position vectors.

 

[gneill]

Is it possible that the tutor suggested the use of cos(37°) rather than sin(37°)?

 

[PeachBanana]

Thanks you two! No, he definitely said (sin 37°).