Why Use the Parallel Axis Theorem with the Second Moment of AREA?

[tomtomtom1]

TL;DR Summary

Why Use The Parallel Axis Theorem For With Second Moment of AREA???

Hi all

I was wondering if someone could help clear up some confusion about the Parallel Axis Theorem.

I am trying to understand the purpose/benefit of applying the Parallel Axis Theorem with respect too the Second Moment Of Area.

For example I have a beam that is under load.

I have found its centroid axis from which i can calculate the second moment of area about the x-axis (using the equation bh^3/12) which would tell me the resistance to bending in about the X axis.

Now if i use the Parallel Axis Theorem to calculate the second moment of area from the base of my shape which is a distance d below the neutral axis then what does that tell me? how does this help me?

Below is a sketch of my thinking?

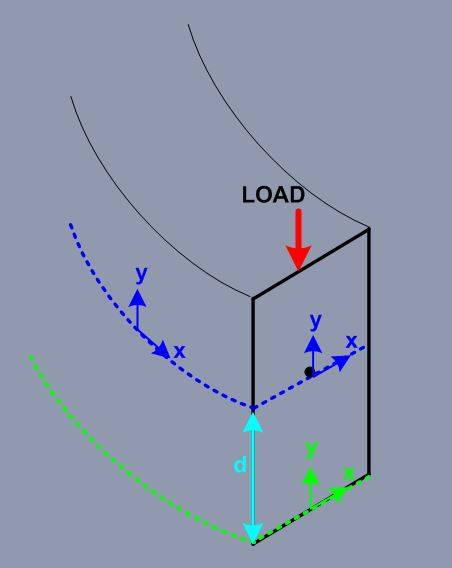I am struggling to understand why taking the second moment of area from somewhere other than the neutral axis helps in anyway.

I know it helps with Second Moment Of Mass but i just want to get my head around applying the Parallel Axis Theorem to Second Moment of Area for now.

Does this make sense?

 

[Dr.D]

You would use the parallel axis theorem to shift to the bottom fiber only if there was a reason to do so, such as combining this section with another. The theorem is never required. Use it only when it helps.

 

[Vigardo]

I think it is usually employed to obtain the second moment of area of more complex cross-sections, e.g. I or H beams, or even arbitrary cross-sections.

 

[Dr.D]

I think it is usually employed to obtain the second moment of area of more complex cross-sections, e.g. I or H beams, or even arbitrary cross-sections.

Yes, this is correct. This particularly often is important for a welded section composed of many simple shapes.