Work Done by Gravity and Derivation of G.P.E.

[Zheng Tien]

I came across this website and I intend to find out more about work done by gravity and derivation of gravitational potential energy (Sorry, the thread name is too long, so I abbreviate it as G.P.E.)

Ok, here is the problem.

I am quite confused with the calculation of work done against gravity and work done by gravity.

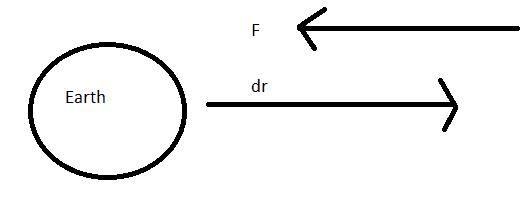
Suppose I have a spacecraft at a distance r₁ from the Earth's center. Then, I move the spacecraft to a distance r₂ from Earth's center. I want to calculate the work done by gravity on the spacecraft .

Here is what I do (Sorry, I don't know how to use LaTeX):

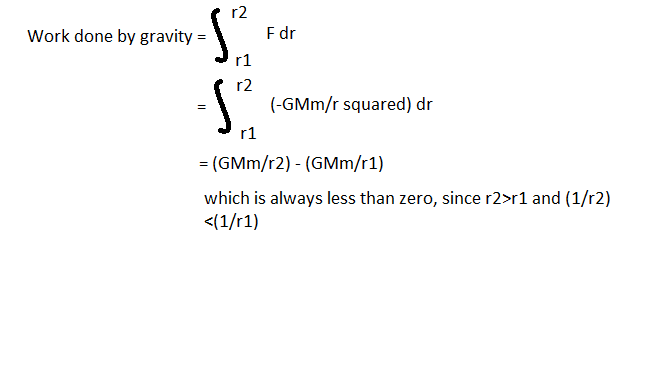
In the above case, I assume that:

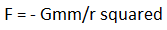
In the second case, which is following the link to the website is this: I bring the S/C from a distance r₂ to r₁.

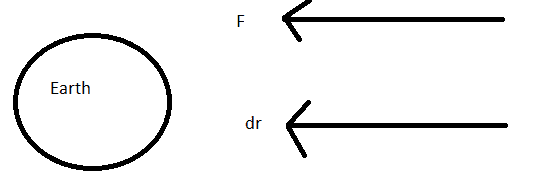
And here is my calculation:

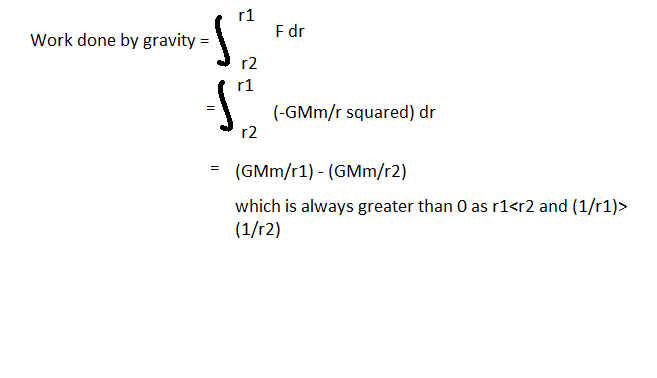
Questions:

1. In the first case, work done by gravity is negative. But I remember there should be a negative sign when calculating work done in my equation (because Force, F and displacement, dr are in opposite direction), why is it that now I don't have to put it but I can get the right answer? Why

2. In the second case, I follow the website link as shown above but the same question pops up, now Force, F and displacement, dr are of the same direction but remember that I define F is opposite in direction to dr, so supposedly there should be a negative sign as well in the formula since now, F is of same direction as dr.

Can anyone tell me my mistake?

Thank you.

The negative signs are frustrating...
Zheng Tien.

 

[Doc Al]

Think of the force of gravity having a magnitude of F and a direction towards the earth. When moving the object away from the earth, the work done by gravity will be negative since the force and displacement are opposite; when moving towards the earth, the work done by gravity will be positive.

 

[Zheng Tien]

Hi Mentor Doc Al.

I can understand what you say.

I understand the concept physically, but not mathematically. I need someone to help me with the maths. Can you explain what is wrong with my mathematics? I suspect I haven't fully comprehend the integration part.

For the first case, where I bring a spacecraft from r1 (closer to Earth) to r2 (further away from Earth), I Integrate from r1 to r2 (integrate from initial position to final position), which makes sense, but when you consider the maths for F (gravity) and dr (displacement), the signs will confuse you easily. The usual definition is F is in the opposite direction of r. So, even when you integrate F with respect to r (dr), there must be a negative sign in the equation since F is opposite in direction to dr, but if you put that into the equation, you get the wrong answer.

What is my mistake here?

Thanks for replying.

Regards,

Zheng Tien.

 

[Doc Al]

"dr" points in the direction of increasing r. The force has a minus sign, since it is directed towards decreasing r. (And r is the variable of integration.)

When integrating from r1 to r2, you'll get a negative answer (as expected) since you are calculating the work done by gravity in moving the object away from the earth. The change of sign when moving towards the Earth is automatically handled by the change in order of the integration limits.

 

[Doc Al]

Your mistake is counting the negative sign twice in the second case. (Or at least being tempted to.) "dr" always points outward.

 

[Zheng Tien]

Ok, let me see if I understand this.

When I am doing integration for work done by gravity or against gravity, I just have to use the integration formula integrate F with respect to r (dr) regardless of whether the object (in our case here, it is the spacecraft ) is moving away or towards Earth.

Then I only have to consider the limits of integration. For objects moving away from Earth (assume r1 is closer to Earth than r2 is), I integrate from r1 to r2 (so, r2 is at the top of the integral sign and r1 is below it, like this:

) and I will get a negative work.

For objects moving closer to Earth, I integrate from r2 to r1 (so, r1 is at the top of the integral sign and r2 is below it, like this:

) and I will get a positive work.

So, all in all, I don't have to bother about the signs of F and dr while doing the integration work, I only have to be concerned with the limits of integration. Am I correct?

But what about our traditional way of viewing things, where we say Work done = F dot s cos (theta). Apparently, theta in our first case (assume gravitational force is constant) would be 180 degrees. So, there would be a negative sign when calculating work done against gravitational force.

Does this mean that the limits of integration already "replace" the function of cos (theta) in this case, i.e. determine the negative work done for the "against gravity" case (the first case, spacecraft getting away from Earth)?

What about if theta is not equal to 180 degrees or 0 degrees and some other values but the force is still variable? Do we need to use vector calculus in this case? (I am only 18 years old, just graduate from high school last year, so I know nothing about vector calculus, but I know vector and calculus separately.)

Thanks for answering.

 

[Zheng Tien]

I think I see it. I notice my mistake in the second case. "dr always points outward." But even if dr points outward, I still integrate from r2 to r1, am I correct, mentor Doc Al?

 

[Doc Al]

I think I see it. I notice my mistake in the second case. "dr always points outward." But even if dr points outward, I still integrate from r2 to r1, am I correct, mentor Doc Al?

Exactly.

 

[Zheng Tien]

Ok, mentor Doc Al, thanks for your reply so far. I will post any further questions here in case I need to.

(I need to sleep now, it is already 10:55 p.m. here in Penang, GMT+ 8 hours)

Thank you.
Zheng Tien.

 

[Doc Al]

You are most welcome!