Work done by gravity - what is wrong?

[Zoli]

I would like the determine the work done by gravity on a mass attached to a rod (see the attached image). The rod is assumed to be weightless and rigid.
I start from the definition of work:
$$W_{AB} = \int_{\mathbf{r}_A}^{\mathbf{r}_B} \mathbf{G}\cdot \mathrm{d}\,\mathbf{r}.$$
In the x-y coordinate system we can write
$$\mathbf{G} = G(0,-1), \quad \mathrm{d}\,\mathbf{r} = R(\sin\varphi,-\cos\varphi)\mathrm{d}\,\varphi,$$

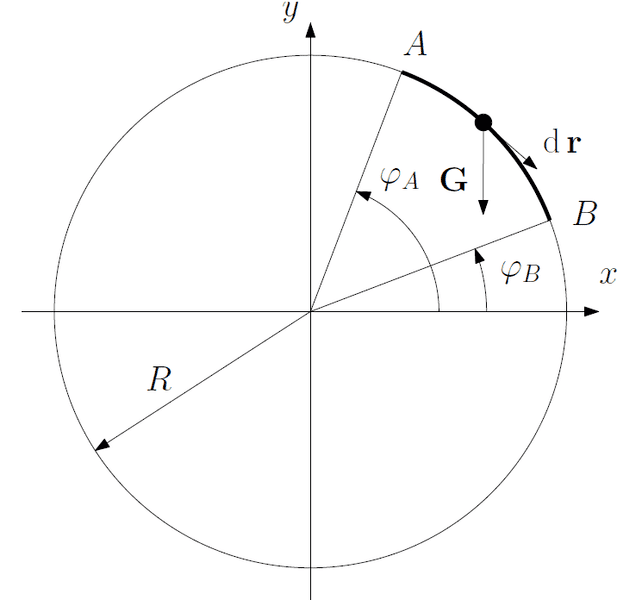
therefore the value of the integral becomes $W_{AB} = GR(\sin\varphi_B - \sin\varphi_A),$ which is negative since we are in the first quadrant. However, if we look at the attached draft, we may notice that the angle between $W_{AB} = \mathbf{G}$ and $\mathrm{d}\,\mathbf{r}$ is an acute angle, so the work should be positive.
What have I done wrong?

Thank you, Zoli

 

[PhanthomJay]

You tried it the hard way and in so doing, looks like you integrated backwards. The easier way is to note that the work done by gravity is independent of the path taken, and equal to the negative of the potential energy change. You can calculate the potential energy from basic trig to determine the vertical height change. Since the gravity force and it's vertical displacement are in same direction, work must be positive.

 

[athosanian]

I see it. It should be noticed that dr=-R(sinφ,−cosφ)dφ,becasue from A to B dφ is negative.

 

[Zoli]

You tried it the hard way and in so doing, looks like you integrated backwards. The easier way is to note that the work done by gravity is independent of the path taken, and equal to the negative of the potential energy change. You can calculate the potential energy from basic trig to determine the vertical height change. Since the gravity force and it's vertical displacement are in same direction, work must be positive.

Yes, I surmised that I changed the path of integration, since $\mathrm{d}\,\varphi$ is negative. I forgot the idea of the potential function. Thank you.

 

[PJC01]

First of all, it is important to clarify that work done by gravity is a scalar quantity and does not have a direction associated with it. This means that the negative sign in your calculation does not necessarily indicate a negative value for the work done.

Additionally, in the definition of work you have provided, the force of gravity, represented by \mathbf{G}, should be multiplied by the displacement \mathrm{d}\,\mathbf{r}, not the position vector \mathbf{r}. This would result in a positive value for the work done, as it should be.

Furthermore, it is important to note that the angle between the force of gravity and the displacement vector should be the angle between the two vectors at each point along the path, not just at the initial and final points. This means that the angle should vary as the mass moves along the rod, and the integral should be evaluated accordingly.

Finally, it is important to consider the assumptions made in the problem statement. If the rod is assumed to be weightless and rigid, it cannot be affected by the force of gravity and therefore the work done by gravity would be zero. This is because work is defined as the force applied over a distance, and if the rod does not move, no work is being done.

In summary, it is important to carefully consider the definitions and assumptions when calculating work done by any force, including gravity. It is also important to keep in mind that work is a scalar quantity and does not have a direction associated with it.