- #1
Zoli
- 20
- 0
I would like the determine the work done by gravity on a mass attached to a rod (see the attached image). The rod is assumed to be weightless and rigid.
I start from the definition of work:
[tex] W_{AB} = \int_{\mathbf{r}_A}^{\mathbf{r}_B} \mathbf{G}\cdot \mathrm{d}\,\mathbf{r}.[/tex]
In the x-y coordinate system we can write
[tex] \mathbf{G} = G(0,-1), \quad \mathrm{d}\,\mathbf{r} = R(\sin\varphi,-\cos\varphi)\mathrm{d}\,\varphi, [/tex]
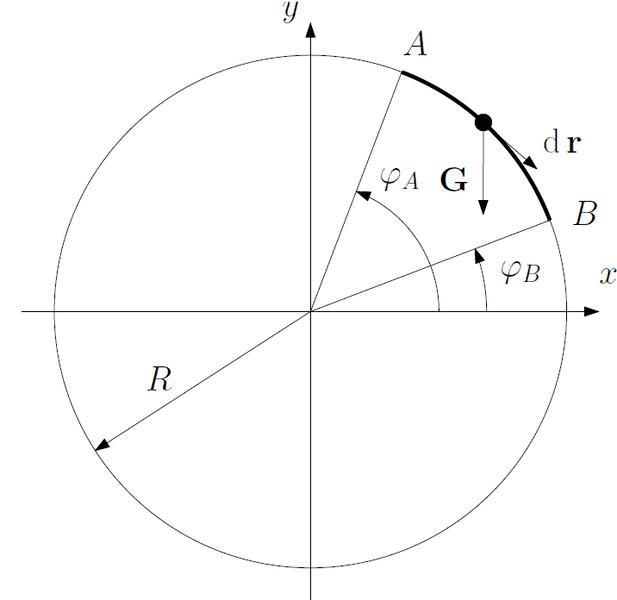
therefore the value of the integral becomes [itex] W_{AB} = GR(\sin\varphi_B - \sin\varphi_A), [/itex] which is negative since we are in the first quadrant. However, if we look at the attached draft, we may notice that the angle between [itex] W_{AB} = \mathbf{G} [/itex] and [itex] \mathrm{d}\,\mathbf{r} [/itex] is an acute angle, so the work should be positive.
What have I done wrong?
Thank you, Zoli
I start from the definition of work:
[tex] W_{AB} = \int_{\mathbf{r}_A}^{\mathbf{r}_B} \mathbf{G}\cdot \mathrm{d}\,\mathbf{r}.[/tex]
In the x-y coordinate system we can write
[tex] \mathbf{G} = G(0,-1), \quad \mathrm{d}\,\mathbf{r} = R(\sin\varphi,-\cos\varphi)\mathrm{d}\,\varphi, [/tex]
therefore the value of the integral becomes [itex] W_{AB} = GR(\sin\varphi_B - \sin\varphi_A), [/itex] which is negative since we are in the first quadrant. However, if we look at the attached draft, we may notice that the angle between [itex] W_{AB} = \mathbf{G} [/itex] and [itex] \mathrm{d}\,\mathbf{r} [/itex] is an acute angle, so the work should be positive.
What have I done wrong?
Thank you, Zoli