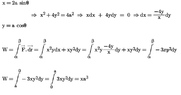- 42,785
- 10,490
That's worrying. If you do try that be careful not to use θ for both purposes. Either take the polar coordinates to be (r,φ) or change the given parameter from θ to t, say. I say it is worrying because it makes me wonder whether your teacher has blundered.
If you draw a line from the origin to a point half way along the horizontal dashed blue line, the angle between that and the y-axis is the given theta.
No, neither of them matches the given theta. The one you circled would give ##x=r\cos(\theta), y=r\sin(\theta), y/x=\tan(\theta)##. But you are given ##y/x= \frac 12\cot(\theta)##.MatinSAR said:Thank you but what do you mean by this ?! I didn't understand.
View attachment 317261
This one should be Theta ...
If you draw a line from the origin to a point half way along the horizontal dashed blue line, the angle between that and the y-axis is the given theta.