- #1
navneet9431
Gold Member
- 107
- 9
Homework Statement
See the explanation of work done by variable forces given in my textbook.
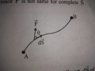
For calculation of work done by variable forces the author analyses only a small fraction of displacement "ds".
And then he makes **assumption** that the force is acting on the particle at an angle theta and that too in the *upward* direction.And then he integrates them.
My question is how integrating them would give us the total work done by the variable force.Because at different positions the angle at which the force is acting would change.It would not be 'theta' for all instants.
And my next question is that how should we determine in which direction the force is acting?
Like in my book the author assumed that it would act like this(in the upward direction),
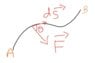
So what if I say that the force would not act like that but would act like this in the downward direction?
Homework Equations
W=Fcos(theta)*S
The Attempt at a Solution
I think that the direction of force should be determined by the curve if the path.If the path bends inwards then the force would act downwards and if the path is bending upwards then the force would act upwards.
Is my thinking correct?
I will be thankful for any help!