Travis Enigma
- 13
- 4
- Homework Statement
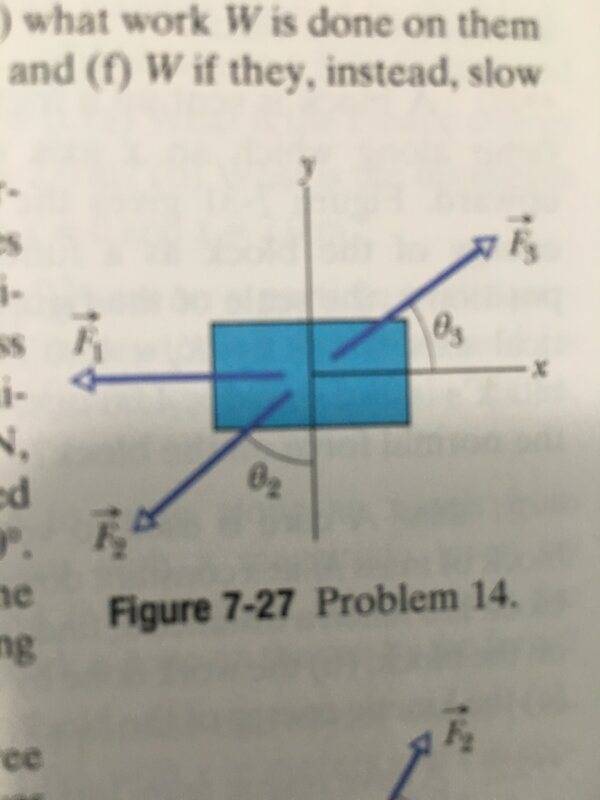
- The figure shows an overhead view of three horizontal forces acting on a cargo canister that was initially stationary but now moves across a frictionless floor. The force magnitudes are F1 = 3.00 N, F2 = 4.00 N, and F3 = 10.0 N, and the indicated angles are θ2 = 50.0˚ and θ3 = 35.0˚. What is the net work done on the canister by the three forces during the first 4.00 m of displacement?
- Relevant Equations
- W= F*d*cos(theta)
Here's a diagram of the object
 My Question: My friend and I were solving this problem. We both found Fxnet and Fynet. However to find work I did W= Fnet*d whereas he did W= Fxnet* d. He claims that since it's sliding on the floor it can only go in the x-direction, and it can't go in the y-direction. Which one of us is right?
My Question: My friend and I were solving this problem. We both found Fxnet and Fynet. However to find work I did W= Fnet*d whereas he did W= Fxnet* d. He claims that since it's sliding on the floor it can only go in the x-direction, and it can't go in the y-direction. Which one of us is right?
My 2nd Question: I always thought the following x-axis: left and right, y-axis: forward and backward, z-axis: up and down. Is this right? If so, then how come my friend is telling me it's impossible for it to go in the y-axis because it can't go up since it sliding on a horizontal plane?
My 2nd Question: I always thought the following x-axis: left and right, y-axis: forward and backward, z-axis: up and down. Is this right? If so, then how come my friend is telling me it's impossible for it to go in the y-axis because it can't go up since it sliding on a horizontal plane?