Work done on moving a submerged object

AI Thread Summary
The discussion focuses on calculating the work done on a submerged object by first determining the buoyant force (Fb) and gravitational force (Fg) acting on the tank. The net force equation (Fnet = Fb - Fg - T = 0) is used to find the tension (T) as 9751. The participant considers calculating work done as the product of tension and distance (9751 x 50.4) but expresses uncertainty about this approach. Another contributor points out the importance of including units in calculations, suggesting that omitting them could result in a loss of marks. Accurate calculations and proper unit notation are essential for scoring well in physics problems.
Murray Inglis
Messages
2
Reaction score
0
Homework Statement
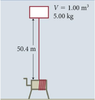
A 5.00 kg air-filled, sealed, rigid float tank that has a volume of 1.00 m3
is pulled 50.4 m
down to the seafloor in order to assist in lifting a sunken object. A diver standing on the
seafloor cranks a winch to pull the tank down.
How much work is required to pull the tank down? (You may safely ignore the mass
in the air tank and the mass of the winch rope.)
Relevant Equations
Fb = p(rho)Vg
I first worked out the buoyant force using rho = 1000, g = 9.8 and V = 1. (this gives Fb = 9800)
I then worked out Fg of the tank (5 x 9.8 = 49)
Then I used Fnet = Fb - Fg - T = 0 to work out tension as 9751.
I thought the work done would be the work done by tension (9751 x 50.4), but I'm not sure if this works.
 

Attachments

  • Screenshot 2021-09-27 122851.png
    Screenshot 2021-09-27 122851.png
    6 KB · Views: 165
Physics news on Phys.org
Murray Inglis said:
I thought the work done would be the work done by tension (9751 x 50.4), but I'm not sure if this works.
Sounds good to me.
 
Doc Al said:
Sounds good to me.
Oh great, thanks. It was a 7 mark question so it just felt like I was missing something.
 
Murray Inglis said:
Oh great, thanks. It was a 7 mark question so it just felt like I was missing something.
You are missing the units next to the numbers you provided. If I were scoring this, I would subtract at least 1 mark for this.
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Work done by a force down a ramp
Replies
11
Views
2K
What Is the Connection Between Buoyancy and Apparent Mass?
Replies
2
Views
1K
Spring constant formlula for Force and Work Done
Replies
12
Views
2K
My Mistake? Understanding Friction Force & Work Done on Snowy & Icy Surfaces
Replies
29
Views
2K
Calculating Buoyancy Force & Length of Submerged Cube
Replies
11
Views
2K
Work calculation for lifting a Tetrahedron-shaped object from the water
Replies
37
Views
3K
About work done through exercise (push ups)
Replies
4
Views
3K
Yes, that makes sense. Thank you for pointing that out.
Replies
8
Views
2K
I calculating the buoyancy force
Replies
10
Views
2K
Work done on a conical pendulum
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top