Callmelucky
- 144
- 30
- Homework Statement
- Is it possible to make machine that would take more heat from hot reservoir to do work than what would hot reservoir give to cold reservoir(heat)?
- Relevant Equations
- 1st law of thermodynamics
photo below... Is it possible to make a machine that would take more heat from the hot reservoir to do work than what would hot reservoir give to the cold reservoir(heat)? Apparently, it's impossible because it violates 1st law of thermodynamics.
the thickness of the arrows symbolizes the amount of heat or work. The red rectangle is hot res. the blue rectangle is cold res. The grey circle is a working tool(mean).
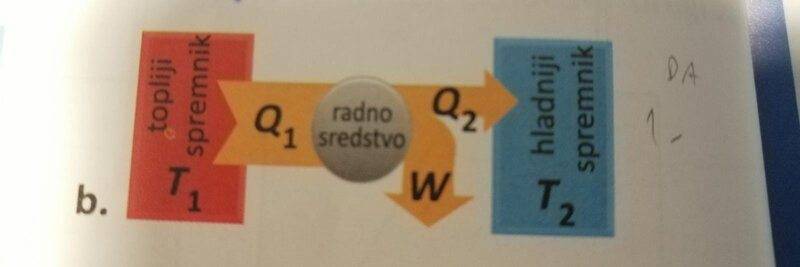
the thickness of the arrows symbolizes the amount of heat or work. The red rectangle is hot res. the blue rectangle is cold res. The grey circle is a working tool(mean).
