Work required to attach the bowstring to the bow?

[SLTH02]

Homework Statement

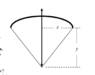
A ballista is essentially a very large bow and arrow, except that it fires 3-m long, 2-kg arrows. The arrows are propelled by the stretched bowstring and bow, which behave as if they are two nonlinear springs that each behave according to the equation
F = -kx1.5, where the force constant k = 500 N·m-1.5 and equilibrium length l = 0.5 m. The ballista is cocked, so that the distances x and y are 1.0 m and 1.3 m, respectively. A constant 10-N frictional force opposes all motion of the arrow. The arrow is shot straight upwards. As the arrow moves upward, the distance y changes but the distance x does not.

The answer is suppose to be 70.7 J

Relevant Equations

WK = Fdcos(x)
Work done by non conservative force = change in mechanical energy

E final = (1/2)(500)(1.14012)^2 = 324.968 J
E initial = (1/2)(500)(0.5)^2 = 62.5 J

E final - E initial = 262.468 J

 

[scottdave]

It looks to me that you have a right triangle, and the length is the hypotenuse.
So initial length of the Right side is √(x² + y²) = √((1.0m)² + (1.3m)²). To find the Force, you need to consider the difference between the actual length and equilibrium length.
The Left side will have the same magnitude but (x) components cancel. The y components will add. I think you are going to have to come up with an expression for F_y then integrate Fdy to get the work done.

Remember to consider the net force acting on the "arrow" (tension and friction).

What I am not sure of (maybe there is more information that you have not given), if the equilibrium length is 0.5m the total length of the cord is 1.0m, yet from the picture, it seems that when released the cord will be 2 meters long.

 

[haruspex]

then integrate Fdy to get the work done.

I suggest calculating the work done against friction, in the obvious way, and integrating kx^1.5 to find the work done by the cord spring.

the total length of the cord is 1.0m, yet from the picture, it seems that when released the cord will be 2 meters long.

That seems right - the cord does not end relaxed.

 

[scottdave]

That seems right - the cord does not end relaxed.

I'm just not seeing how the cord will ever get down to 1.0 meter (twice of 0.5 m). I guess I'm just missing something. I better go back to my Bayesian Statistics homework.

 

[haruspex]

I'm just not seeing how the cord will ever get down to 1.0 meter

Why does it need to?

 

[scottdave]

Why does it need to?

OK, so they're saying it always has some tension on it. Now I see. Thanks.

 

[SLTH02]

The Left side will have the same magnitude but (x) components cancel. The y components will add. I think you are going to have to come up with an expression for Fy then integrate Fdy to get the work done.

Thanks! Didn't thought about x components cancel