Work to bring a charge to the center of two quarter circles

[lorenz0]

Homework Statement

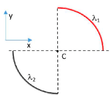
Find the electric field at point C, which corresponds to the center of the two arcs of circumference with radius $𝑅 = 10 cm$ with uniform charge densities $\lambda_1 = + 1nC / m$ and $\lambda_2 = -1 nC / m$ respectively.
Also find the work required to bring a charge $q= 5 \mu C$ from infinity to point C.

Relevant Equations

$\vec{E}=\frac{kq}{r^2},\ V(r)=\frac{kq}{r}$

By measuring angle \theta from the positive $x$ axis counterclockwise as usual, I get $d\vec{E}=k( (\lambda_2-\lambda_1)\cos(\theta)d\theta, (\lambda_2-\lambda_1)\sin(\theta)d\theta )$ and by integrating from $\theta=0$ to $\theta=\frac{\pi}{2}$ I get $\vec{E}(P)=\frac{k(\lambda_1-\lambda_2)}{R}(-1,-1)$.

Now, the work to bring a charge from infinity to point P should be (if we set $V(\infty)=0$) $L=qV(P)=q\int_{\theta=0}^{\theta=\pi/2}(\frac{k\lambda_1}{R}+\frac{k\lambda_2}{R})Rd\theta=0$

I am a bit unsure about the work being $0$, it doesn't feel intuitive to me that it should be: is this correct? Is there an intuitive explanation for the work being $0$? Thanks

 

[haruspex]

Please post either a diagram or a full description of the arc arrangement.
But just looking at the last line, I do not see how you get zero from that integral.

 

[lorenz0]

Please post either a diagram or a full description of the arc arrangement.
But just looking at the last line, I do not see how you get zero from that integral.

I have posted the diagram; I get zero since $\lambda_1=-\lambda_2$.

 

[BvU]

Is there an intuitive explanation for the work being 0?

If you bring in the charge from infinity over the line $y = -x$, the electric force is perpendicular to the motion, so no mechanical work is involved.

$\$

 

[lorenz0]

If you bring in the charge from infinity over the line $y = -x$, the electric force is perpendicular to the motion, so no mechanical work is involved.

$\$

I see, thank you very much!