Young's Modulus: 2 bars placed end to end and compressed from both ends

Click For Summary
SUMMARY

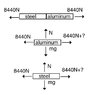
This discussion focuses on calculating the change in length of two bars, one aluminum and one steel, when subjected to a compressive force of 8440 N. The Young's Modulus for aluminum is 7.0 x 1010 Pa, and for steel, it is 2.0 x 1011 Pa. Participants clarify that the force acting on each bar is equal and opposite, emphasizing the importance of using the correct force in calculations. The discussion also highlights the necessity of dividing the force by the cross-sectional area to find stress, which is crucial for determining the change in length.

PREREQUISITES
  • Understanding of Young's Modulus and its application in material science
  • Knowledge of basic mechanics, including Newton's laws of motion
  • Familiarity with stress and strain calculations
  • Ability to draw and interpret free body diagrams (FBDs)
NEXT STEPS
  • Calculate the change in length for both aluminum and steel using the formula ΔL = (F * L) / (A * E)
  • Research the Young's Modulus and Poisson Ratio for copper oxide and ferrous oxide
  • Explore the effects of temperature on the Young's Modulus of materials
  • Learn about composite materials and their mechanical properties
USEFUL FOR

Students in engineering and physics, material scientists, and anyone interested in understanding the mechanical properties of materials under stress.

Angie_Agnes
Messages
23
Reaction score
0

Homework Statement



Two bars, one composed of aluminum and one of steel are place end to end as shown in Figure P11.60. The bars are both initially of length L = 24 cm, and both have a square cross section with h = 3.9 cm. If a compressive force of F = 8440 N is applied to each end, find the change in length of the Aluminum=____________ and Steel=___________

Young's Modululs for Aluminum: 7.0*10^10
Young's Modululs for Steel: 2.0*10^11


Homework Equations



F/A=y (ΔL/L)

The Attempt at a Solution


I don't know how to start on this one...
 

Attachments

  • 11P56.jpeg
    11P56.jpeg
    10.6 KB · Views: 544
Physics news on Phys.org
Draw a FBD of the aluminum...how much doest it compress? Draw a FBD of the steel...how much does it compress?
 
I tried taking the force x2, then using the youngs modulus to try to find ΔL but was getting the wrong answer. Does the compression of the steel affect the side of aluminum that is touching it? do both sides of the bar compress?
 
Angie_Agnes said:
I tried taking the force x2,
What do you mean by 'the force x 2'? What is the force on the aluminum bar? What is the force on the steel bar?
then using the youngs modulus to try to find ΔL
yes
.. Does the compression of the steel affect the side of aluminum that is touching it?
The force of the steel on the aluminum affects it
do both sides of the bar compress?
It doesn't matter. If you had a copper bar fixed at one end to a rigid wall and applied a force F to it, it would compress say 1 mm at your end. If the bar was compessed by you pushing it on one end with a force F and your buddy pushing it with a force F at the other end, it would still compress 1 mm, say 0.5mm at your end and 0.5 mm at your buddy's end. Yeahh, Buddy!
 
Well, the force is applied to both ends, so I took a guess and multiplied the force by 2 and then used that to try to solve for compression of aluminum. Didn't work.
 
For equilibrium, there must be a force at both ends, equal and opposite. But draw a free body diagram that cuts through the rod and around one end. Use Newton 1. The force in any part of the rod, aluminum or steel, is ____??____ N?
 
Normal force-? mg?
 
What I'm having trouble with is how to define the force from the end that would include the other rod- if I'm just looking at the aluminum section, it's got the force pushing on it from one end, 8440 N, and on the other end it has 8440N force pushing in the opposite direction, plus what ever impact it is having on the force of the steel.

Attempt at free body diagram:
 

Attachments

  • FBD.jpg
    FBD.jpg
    19.2 KB · Views: 466
Angie_Agnes said:
What I'm having trouble with is how to define the force from the end that would include the other rod- if I'm just looking at the aluminum section, it's got the force pushing on it from one end, 8440 N, and on the other end it has 8440N force pushing in the opposite direction, plus what ever impact it is having on the force of the steel.

Attempt at free body diagram:
Your free body diagrams assume the rods rest on a frictionless table, which is OK, and they are almost correct and would be completely correct if you got rid of that plus sign (your '8440 N +' Newtons should just read '8440 N'). By Newton's first law, the force of the steel on the aluminum is 8440 N, and by his 3rd law, the force of the aluminum on the steel is 8440 N. There is no additional "+" force. Even when you look at just half of the aluminum bar, the internal force in the bar must be 8440 N, and that force is caused by the push force of the of the other part of the aluminum rod acting on the first part. Don't add them twice.. If the force on the end of the alum section was 8440 + N, the net force on the bar would be greater than 0, but since the bars are at rest once they compress to their at rest position, the net force must be 0.
 
  • #10
I feel like such an idiot. I forgot a key part of the equation when calculating... dividing the force by the area! So that would by why I kept getting the answers wrong on the homework and figured I must be forgetting missing something.
Thanks for your patience and help.
 
  • #11
Can anyone please help me out in finding the Young's modulus and Poisson Ratio of standard copper oxide and Ferrous oxide
 
  • #12
pramodm89 said:
Can anyone please help me out in finding the Young's modulus and Poisson Ratio of standard copper oxide and Ferrous oxide
Start a new thread.
 

Similar threads

Young's modulus — Finding the change in the length of a metal bar under stress
  • · Replies 20 ·
Replies
20
Views
3K
Stretching of a wire due to it's weight
  • · Replies 19 ·
Replies
19
Views
4K
Does Young's Modulus Change When Nano-Tubes Are Connected End-to-End?
  • · Replies 2 ·
Replies
2
Views
1K
Stress, Strain, and Sound in a Projectile Steel Rod
  • · Replies 2 ·
Replies
2
Views
2K
Appying a force bar + Young's Modulus + Force Applied
  • · Replies 3 ·
Replies
3
Views
2K
Temperature of a bar to produce certain force on wall
  • · Replies 6 ·
Replies
6
Views
2K
Femur Compression/Young's Modulus
  • · Replies 7 ·
Replies
7
Views
16K
Young's Modulus Brass Wire Question
  • · Replies 3 ·
Replies
3
Views
2K
Traction/ Compression stress and strain exercise
  • · Replies 1 ·
Replies
1
Views
2K
Finding Young's Modulus for Steel from two graphs
  • · Replies 1 ·
Replies
1
Views
4K