- #1
Vinay080
Gold Member
- 54
- 3
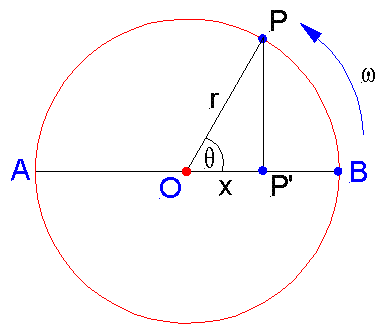
Consider a particle P moving in a circle of radius r as shown in the figure.
Premise 1: Position of the particle can be described by the angle θ.
Premise 2: Particle reaches the position with an angle θ if it has covered the angle lesser than θ.
Premise 3: Particle can never reach non-terminating decimal form radian value.
For example: 0.33333...rad; The particle can never reach this radian value because, to reach this value, first particle needs to cover 0.33 rad, then 0.333 rad, then 0.33333, and so on. Particle needs to go on and on, and the sequence of 0.333.. never ends.
Premise 4: As the particle can never reach non-terminating decimal form radian value, it can't even reach neighbor terminating decimal form radian value. For example 0.4 (considering 0.333.. of Premise 3) can never be reached as 0.333... can never be reached.
The argument, as evident, is in the zeno version. But, I am not able to come out of this cage. What is going wrong in this argument? Can the particle never reach non-terminating decimal form value? I think this problem can be generalized to all the physical quantities.
I had discussed a similar problem here: https://www.physicsforums.com/threads/diagonal-length-problem.806206/
Premise 1: Position of the particle can be described by the angle θ.
Premise 2: Particle reaches the position with an angle θ if it has covered the angle lesser than θ.
Premise 3: Particle can never reach non-terminating decimal form radian value.
For example: 0.33333...rad; The particle can never reach this radian value because, to reach this value, first particle needs to cover 0.33 rad, then 0.333 rad, then 0.33333, and so on. Particle needs to go on and on, and the sequence of 0.333.. never ends.
Premise 4: As the particle can never reach non-terminating decimal form radian value, it can't even reach neighbor terminating decimal form radian value. For example 0.4 (considering 0.333.. of Premise 3) can never be reached as 0.333... can never be reached.
The argument, as evident, is in the zeno version. But, I am not able to come out of this cage. What is going wrong in this argument? Can the particle never reach non-terminating decimal form value? I think this problem can be generalized to all the physical quantities.
I had discussed a similar problem here: https://www.physicsforums.com/threads/diagonal-length-problem.806206/
Last edited: