waveandmatter
- 16
- 0
As i understand it, the Maxwell equations in potential form (in the Lorenz gauge) are basically 4 independent wave equations for the 3 components of A and the 1 component of Phi, with J and ρ acting as source terms:
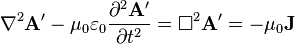
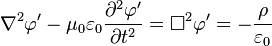
Now from the usual formulation of the Maxwell equations and from experience we know, that an infinitesimally small oscillating current, for example Jx, generates dipole waves, which have nonzero values for all 3 field components.
I can not see, how the 4 independent wave equations of the potential formulation can ever generate Ey or Ez components, if i only plug in a Jx in one point. Contrarily, from the equations i would guess that i would get a spherical wave with only Ex component, since the equation for A works component-wise and the equation that gets me E out of A also only performs a temporal derivation.
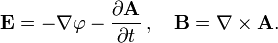
This seems to contradict the idea that the E-vector has to stand at right angles to the k-vector (which in a spherical wave takes all kinds of directions).
The only possible explanation for me would be, that if i incorporate a J, i would also have to add the continuity equation for ρ, ∇J=d/dt ρ, which would give me a scalar potential phi as well, which in turn would generate the other field components.
Is this explanation correct? If not, how can this formulation give me proper results where E is at right angles to k etc?
Now from the usual formulation of the Maxwell equations and from experience we know, that an infinitesimally small oscillating current, for example Jx, generates dipole waves, which have nonzero values for all 3 field components.
I can not see, how the 4 independent wave equations of the potential formulation can ever generate Ey or Ez components, if i only plug in a Jx in one point. Contrarily, from the equations i would guess that i would get a spherical wave with only Ex component, since the equation for A works component-wise and the equation that gets me E out of A also only performs a temporal derivation.
This seems to contradict the idea that the E-vector has to stand at right angles to the k-vector (which in a spherical wave takes all kinds of directions).
The only possible explanation for me would be, that if i incorporate a J, i would also have to add the continuity equation for ρ, ∇J=d/dt ρ, which would give me a scalar potential phi as well, which in turn would generate the other field components.
Is this explanation correct? If not, how can this formulation give me proper results where E is at right angles to k etc?
Last edited: