- #1
Payam30
- 46
- 1
how do calculate send moment of area.
here is the exampel. I do understand the way one calculate Ixx and Iyy and Ixy. the smaller part has thikness t and the biggest part 3t.
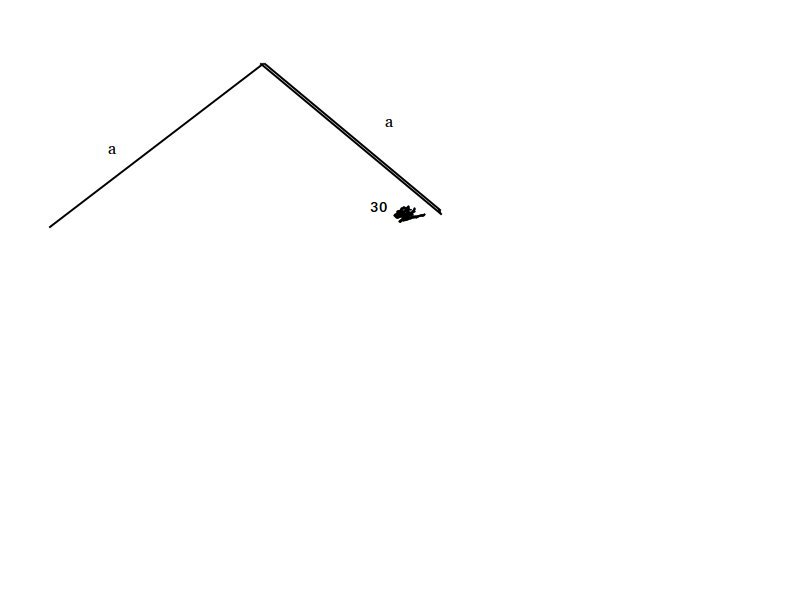
I get :
if you place global coordinate system on the top you will get the position of center of gravity to CG=(3a/8,-a/4).
Now I do: define variable s which is the road
Ixx=∫y²dA=∫t(s sin30)²ds=t[(S³/3)(1/4)]=ta³/12
and we do the same with the right part. and we will get 3ta³/12
Adding these two gives ta³/3. but in the solution they have
(ta³/3)*(1/2)².
I don't get where (1/2)² is comming from.
This is not homework! This is an example from a exam!
here is the exampel. I do understand the way one calculate Ixx and Iyy and Ixy. the smaller part has thikness t and the biggest part 3t.
I get :
if you place global coordinate system on the top you will get the position of center of gravity to CG=(3a/8,-a/4).
Now I do: define variable s which is the road
Ixx=∫y²dA=∫t(s sin30)²ds=t[(S³/3)(1/4)]=ta³/12
and we do the same with the right part. and we will get 3ta³/12
Adding these two gives ta³/3. but in the solution they have
(ta³/3)*(1/2)².
I don't get where (1/2)² is comming from.
This is not homework! This is an example from a exam!
Last edited: