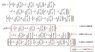- #1
joqhey
- 9
- 0
I found this initial value problem and was supposed to comment on the accuracy of Runge Kutta method. Please enlighten me on the analytic solution.
Find y(2) given the differential equation [itex]\frac{dy}{dx}[/itex]=y[itex]^{2}[/itex]+x[itex]^{2}[/itex] and the initial value y(1)=0.
Thank you.
Find y(2) given the differential equation [itex]\frac{dy}{dx}[/itex]=y[itex]^{2}[/itex]+x[itex]^{2}[/itex] and the initial value y(1)=0.
Thank you.