STENDEC
- 21
- 0
I hope this is self-evident to someone, I'm struggling.
I have a program that draws circles (n-gons really) of various sizes, but by translating-rotating-translating-rotating-..., not by x=sin/y=cos. That works as intended, but my wish is to offset the circle so that its center is (0,0) in the coordinate system. For that i need its center. Currently the circle itself originates from- and hence touches the (0,0) coordinates, so its center is somewhere above, in the y-axis.
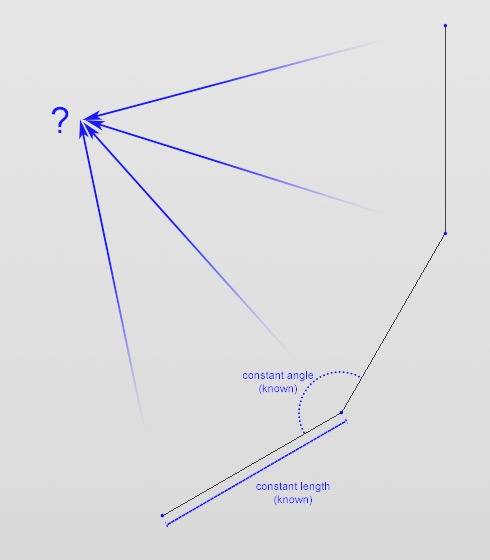
Position of ? is sought after. A wider angle would result in ? rising for instance.
I found lots of tutorials on how to do it on paper using dividers and i also considered that it's a isosceles triangle, but it seems all textbook examples assume that one of the symmetric sides is already known.
I have a program that draws circles (n-gons really) of various sizes, but by translating-rotating-translating-rotating-..., not by x=sin/y=cos. That works as intended, but my wish is to offset the circle so that its center is (0,0) in the coordinate system. For that i need its center. Currently the circle itself originates from- and hence touches the (0,0) coordinates, so its center is somewhere above, in the y-axis.
Position of ? is sought after. A wider angle would result in ? rising for instance.
I found lots of tutorials on how to do it on paper using dividers and i also considered that it's a isosceles triangle, but it seems all textbook examples assume that one of the symmetric sides is already known.