- #1
schafspelz
- 5
- 0
I am confused with a couple of terms usually used in the context of non-radiative transitions. I believe that I understand the concept of diabatic and adiabatic states described in
http://en.wikipedia.org/wiki/Adiabatic_theorem. The basic finding is that the coupling terms in the Hamiltonian matrix (in the basis of the diabatic states) result in an avoided crossing.
I want to transfer this finding to the case of the Born-Oppenheimer approximation, which is said to break down in the region around a level-crossing. And this is actually the point where I come across my first problem. When neglecting the first and the off-diagonal elements (closely related to the non-adiabacity operator), do I get diabatic states (case A) or adiabatic states (case B)?
If the case A is valid, the situation as depicted below would seem logical.

Here we face a level crossing, which is regarded as the breakdown of the Born-Oppenheimer approximation. As soon as the off-diagonals elements taken into account again, the avoided crossing would be obtained then.
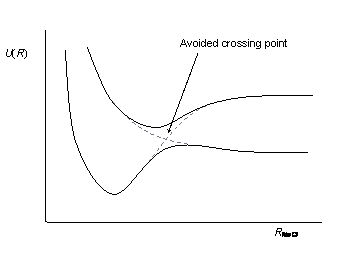
But from my literature search I get the impression that Born-Oppenheimer approximation leads to adiabatic states. But what is the breakdown of the Born-Oppenheimer approximation then? And what are the non-adiabatic transitions resulting from the non-adiabacity operator in the last figure?
I hope anybody can resolve my problems with this stuff!
http://en.wikipedia.org/wiki/Adiabatic_theorem. The basic finding is that the coupling terms in the Hamiltonian matrix (in the basis of the diabatic states) result in an avoided crossing.
I want to transfer this finding to the case of the Born-Oppenheimer approximation, which is said to break down in the region around a level-crossing. And this is actually the point where I come across my first problem. When neglecting the first and the off-diagonal elements (closely related to the non-adiabacity operator), do I get diabatic states (case A) or adiabatic states (case B)?
If the case A is valid, the situation as depicted below would seem logical.
Here we face a level crossing, which is regarded as the breakdown of the Born-Oppenheimer approximation. As soon as the off-diagonals elements taken into account again, the avoided crossing would be obtained then.
But from my literature search I get the impression that Born-Oppenheimer approximation leads to adiabatic states. But what is the breakdown of the Born-Oppenheimer approximation then? And what are the non-adiabatic transitions resulting from the non-adiabacity operator in the last figure?
I hope anybody can resolve my problems with this stuff!