- #1
uzman1243
- 80
- 1
I know its easier to use the substitution method, by I'm trying to see how it'll work for integration by parts. I follow the LIATE method for integration by parts.
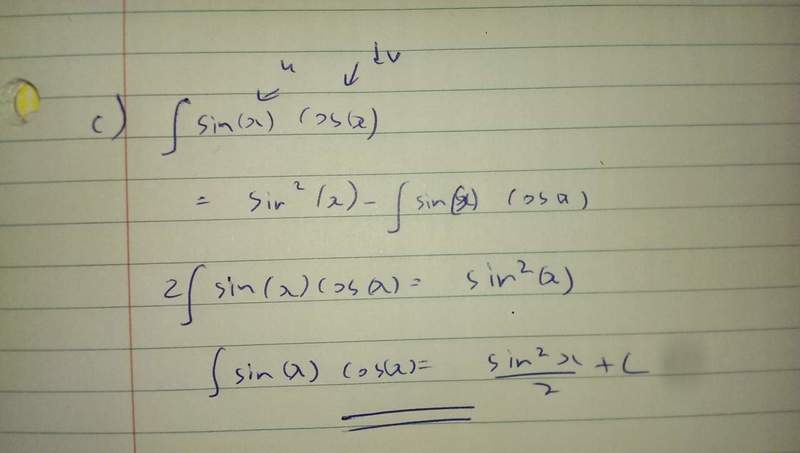
Now if I take u=cos(x) and dv = sin(x), the answer changes.
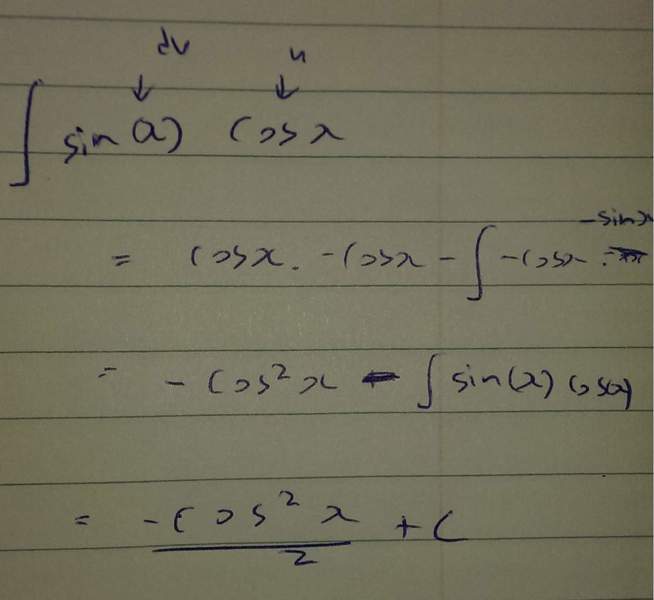
Can you please explain this to me? Which is the 'right' answer?
Now if I take u=cos(x) and dv = sin(x), the answer changes.
Can you please explain this to me? Which is the 'right' answer?

