- #1
Math Amateur
Gold Member
MHB
- 3,990
- 48
I am reading Martin Crossley's book, Essential Topology.
Example 5.43 on page 74 reads as follows:

I am really struggling to get a good sense of why/how/wherefore Crossley came up with the maps f and g in EXAMPLE 5.43. How did he arrive at these maps?
Why/how does f map [itex] S^1 \times S^1 [/itex] onto [itex] T^2 [/itex] and how does one check/prove that this is in fact a valid mapping between these topological spaces.
Can anyone help in making the origins of these maps clear or perhaps just indicate the logic behind their design and construction? I am completely lacking a sense or intuition for this example at the moment ... ...
Definitions for [itex] T^2 [/itex] and [itex] S^1 [/itex] are as follows:

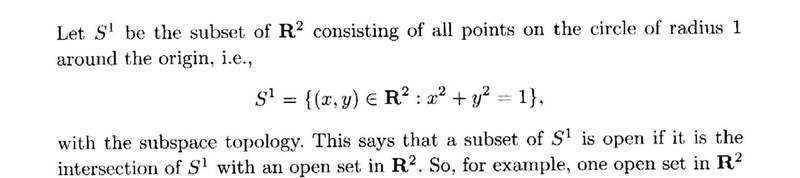
My ideas on how Crossley came up with f and g are totally bankrupt ... but to validate f (that is to check that it actually maps a point of [itex] S^1 \times S^1 [/itex] onto [itex] T^2 [/itex] - leaving out for the moment the concerns of showing that f is a continuous bijection ... ... I suppose one would take account of the fact that (x,y) and (x',y') are points of [itex] S^1 [/itex] and so we have:
[itex] x^2 + y^2 = 1 [/itex] ... ... ... ... (1)
and
[itex] x'^2 + y'^2 = 1 [/itex] ... ... ... ... (2)
Then, keeping this in mind check that
[itex] ((x' +2)x, (x' +2)y, y'[/itex] is actually a point on the equation for [itex] T^2 [/itex], namely:
[itex] x^2 + y^2 + z^2 - 4 \sqrt{x^2 + y^2} = -3 [/itex] ... ... ... (3)
So in (3) we must:
- replace x by (x' +2)x
- replace y by (x' +2)y
- replace z by y'
and then simplify and if necessary use (1) (2) to finally get -3.
Is that correct? Or am I just totally confused ?
Can someone please help?
Peter
Example 5.43 on page 74 reads as follows:
I am really struggling to get a good sense of why/how/wherefore Crossley came up with the maps f and g in EXAMPLE 5.43. How did he arrive at these maps?
Why/how does f map [itex] S^1 \times S^1 [/itex] onto [itex] T^2 [/itex] and how does one check/prove that this is in fact a valid mapping between these topological spaces.
Can anyone help in making the origins of these maps clear or perhaps just indicate the logic behind their design and construction? I am completely lacking a sense or intuition for this example at the moment ... ...
Definitions for [itex] T^2 [/itex] and [itex] S^1 [/itex] are as follows:
My ideas on how Crossley came up with f and g are totally bankrupt ... but to validate f (that is to check that it actually maps a point of [itex] S^1 \times S^1 [/itex] onto [itex] T^2 [/itex] - leaving out for the moment the concerns of showing that f is a continuous bijection ... ... I suppose one would take account of the fact that (x,y) and (x',y') are points of [itex] S^1 [/itex] and so we have:
[itex] x^2 + y^2 = 1 [/itex] ... ... ... ... (1)
and
[itex] x'^2 + y'^2 = 1 [/itex] ... ... ... ... (2)
Then, keeping this in mind check that
[itex] ((x' +2)x, (x' +2)y, y'[/itex] is actually a point on the equation for [itex] T^2 [/itex], namely:
[itex] x^2 + y^2 + z^2 - 4 \sqrt{x^2 + y^2} = -3 [/itex] ... ... ... (3)
So in (3) we must:
- replace x by (x' +2)x
- replace y by (x' +2)y
- replace z by y'
and then simplify and if necessary use (1) (2) to finally get -3.
Is that correct? Or am I just totally confused ?
Can someone please help?
Peter
