- #1
highschoolphys
- 21
- 0
Let's say a student does a simple experiment where she conducts 10 trials at each x value (at each value of the independent variable). She collects data over 30 x values, giving her 300 total trials. For each of the 30 x values, she averages the 10 y values and she calculates the standard deviation in those 10 y values. She makes a plot of average y vs. x in Excel, and uses the standard deviations for y error bars. Assume the plot is linear. Assume there's no error/uncertainty in individual x values. Perhaps also assume the individual y errors are all uniformly distributed and equal. I want this to be a simplest possible case.
Next, the student (a) adds a linear trendline in Excel, (b) has Excel calculate the slope of her line of best fit, and (c) has Excel calculate the standard error in the slope.
I have three questions:
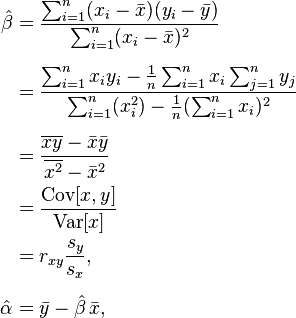
Next, the student (a) adds a linear trendline in Excel, (b) has Excel calculate the slope of her line of best fit, and (c) has Excel calculate the standard error in the slope.
I have three questions:
- Why doesn't the standard error in the slope use the individual y uncertainties as inputs to its calculation? What is the theoretical basis for using a standard error calculation that ignores the individual y measurement errors/uncertainties?
- Does the standard error in the slope fail to represent something crucial about the uncertainty in the slope, due to the fact that the standard error calculation ignores the individual y measurement uncertainties?
- Assume the student uses the equation from the top line (below) to calculate manually the slope of her best fit line. She then uses the rules of uncertainty propagation to propagate the individual y measurement uncertainties through this equation. In so doing, she obtains a value of uncertainty in the slope. How would this value compare to the Excel-calculated standard error in the slope?