- #1
marschmellow
- 49
- 0
Question 1: How does the metric relate to the light cone at a particular point? Obviously, the metric should determine the shape of the light cone, but is the converse true? Does the orientation and width of the light cone tell you everything about the metric? I'm guessing not due to the different degrees of freedom, but can anyone articulate a concise relationship between the two?
Question 2: I've looked at these two sources about Van Stockum Dust and seem to have encountered an internal contradiction. Is anything wrong here?
http://rampke.de/data/2009/12/ba.pdf (pages 7 and 8)
http://en.wikipedia.org/wiki/Van_Stockum_dust
The frame field transformation defined from basis vectors to frame vectors does not seem to be the inverse of the frame field transformation from basis 1-forms to frame 1-forms. If you write out the transformations
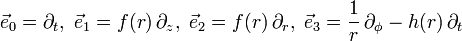
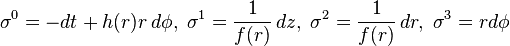
as matrices, you get, respectively:
\begin{pmatrix}1 & 0 & 0 & 0 \\ 0 & f(r) & 0 & 0 \\ 0 & 0 & f(r) & 0 \\ -h(r) & 0 & 0 & \frac{1}{r} \end{pmatrix}
\begin{pmatrix}-1 & 0 & 0 & h(r)r \\ 0 & \frac{1}{f(r)} & 0 & 0 \\ 0 & 0 & \frac{1}{f(r)} & 0 \\ 0 & 0 & 0 & r \end{pmatrix}
Their product is clearly not the identity, but isn't it always true that any change of coordinates does the opposite thing to the basis covectors as it does to the basis vectors? What's going on here?
Thanks in advance!
Question 2: I've looked at these two sources about Van Stockum Dust and seem to have encountered an internal contradiction. Is anything wrong here?
http://rampke.de/data/2009/12/ba.pdf (pages 7 and 8)
http://en.wikipedia.org/wiki/Van_Stockum_dust
The frame field transformation defined from basis vectors to frame vectors does not seem to be the inverse of the frame field transformation from basis 1-forms to frame 1-forms. If you write out the transformations
as matrices, you get, respectively:
\begin{pmatrix}1 & 0 & 0 & 0 \\ 0 & f(r) & 0 & 0 \\ 0 & 0 & f(r) & 0 \\ -h(r) & 0 & 0 & \frac{1}{r} \end{pmatrix}
\begin{pmatrix}-1 & 0 & 0 & h(r)r \\ 0 & \frac{1}{f(r)} & 0 & 0 \\ 0 & 0 & \frac{1}{f(r)} & 0 \\ 0 & 0 & 0 & r \end{pmatrix}
Their product is clearly not the identity, but isn't it always true that any change of coordinates does the opposite thing to the basis covectors as it does to the basis vectors? What's going on here?
Thanks in advance!